练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    若，那么x+y＝_________

    2 【解析】∵， ∴2?x=0，y=0， ∴x=2，y=0； 故x+y=2. 故答案为：2.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017年内蒙古中考数学二模试卷 题型：单选题

    如图所示，数轴上两点A，B分别表示实数a，b，则下列四个数中最大的一个数是（   ）

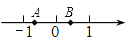
    A. a     B. b   C. 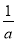D.

    D 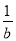【解析】∵负数小于正数， ∴＜a＜b＜ ， 在区间（0，1）上的实数的倒数比实数本身大． 所以＞b． 故选D．

    查看答案和解析>>

    科目：初中数学 来源：江苏省盐城市阜宁县2018届九年级上学期期末考试数学试卷 题型：填空题

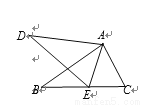
    如图∠DAB＝∠CAE，请补充一个条件：________________，使△ABC∽△ADE．

    ∠D=∠B 【解析】试题分析：当∠D=∠B或∠AED=∠C或AD：AB=AE：AC或AD•AC=AB•AE时两三角形相似．

    查看答案和解析>>

    科目：初中数学 来源：四川省数学八年级下册期末复习测试卷 题型：解答题

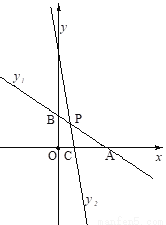
    如图，在平面直角坐标系xOy中，一次函数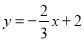与x轴、y轴分别相交于点A和点B，直线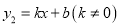经过点C（1，0）且与线段AB交于点P，并把△ABO分成两部分．

    （1）求△ABO的面积；

    （2）若△ABO被直线CP分成的两部分的面积相等，求点P的坐标及直线CP的函数表达式。

    （1）；（2）P()；（3）直线CP的函数表达式为y=-6x+6． 【解析】（1）已知直线y1的解析式，分别令x=0，y=0求出A，B的坐标，继而求出S△ABO． （2）由（1）得S△ABO，推出S△APC的面积为，求出yp=，继而求出点P的坐标，依题意可知点C，P的坐标，联立方程组求出k，b的值后求出函数解析式．

    查看答案和解析>>

    科目：初中数学 来源：四川省数学八年级下册期末复习测试卷 题型：填空题

    如图，在平面直角坐标系中，网格中每一个小正方形的边长为1个单位长度，

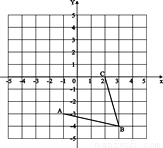
    （1）写出点D的坐标_____________；

    （2）线段BC的长为____________；

    （3）菱形ABCD的面积为____________．

    （1）D（－2，1） （2） （3）15 【解析】(1)菱形ABCD如图所示,D(?2,1)； (2)由勾股定理得,BC==； (3)S菱形ABCD=2S△ABC,=2(4×4?×3×3?×1×4?×1×4)=2(16?4.5?2?2)=2×7.5=15， 故答案为：(1)(?2，1)；(2) ；(3)15.

    查看答案和解析>>

    科目：初中数学 来源：四川省数学八年级下册期末复习测试卷 题型：单选题

    在平面直角坐标系中，平行四边形ABCD的顶点A，B，D的坐标分别是（0，0），（5，0），（2，3），则顶点C的坐标是（　　）

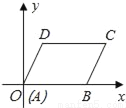
    A. （3，7） B. （5，3） C. （7，3） D. （8，2）

    C 【解析】试题分析：□ABCD的顶点A（0，0），B（5，0），所以AB//CD,AB=5，又D（2，3），所以点C的坐标是（7，3），故选：C.

    查看答案和解析>>

    科目：初中数学 来源：四川省数学八年级下册期末复习测试卷 题型：单选题

    能判定一个四边形是菱形的条件是（ ）

    A. 对角线相等且互相垂直 B. 对角线相等且互相平分

    C. 对角线互相垂直 D. 对角线互相垂直平分

    D 【解析】菱形的判定方法有三种：①定义：一组邻边相等的平行四边形是菱形；②四边相等； ③对角线互相垂直平分的四边形是菱形．只有D能判定为是菱形， 故选D．

    查看答案和解析>>

    科目：初中数学 来源：2017年广东省佛山市中考数学模拟试卷（3） 题型：单选题

    某人到瓷砖商店去买一种多边形形状的瓷砖，用来铺设无缝地板，他购买的瓷砖形状不能是（ ）

    A.正三角形 B.正方形 C.正五边形 D.正六边形

    C 【解析】 试题分析：先分别计算出每一个多边形的内角，再分析是否能整除360°即可． A、正三角形的每个内角是60°，能整除360°，能用来铺设无缝地板， B、正方形的每个内角是90°，能整除360°，能用来铺设无缝地板，D、正六边形的每个内角是120°，能整除360°，能用来铺设无缝地板，均不符合题意； C、正五边形每个内角是180°-360°÷5=108°，不能整除3...

    查看答案和解析>>

    科目：初中数学 来源：黑龙江省2017-2018学年八年级数学上学期期末试卷 题型：单选题

    如图，∠A=15°，AB=BC=CD=DE=EF，则∠DEF等于（ ）

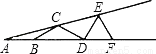
    A．90° B．75° C．70° D．60°

    D 【解析】 试题分析:根据已知条件，利用等腰三角形的性质及三角形的内角和外角之间的关系进行计算． 【解析】 ∵AB=BC=CD=DE=EF，∠A=15°， ∴∠BCA=∠A=15°， ∴∠CBD=∠BDC=∠BCA+∠A=15°+15°=30°， ∴∠BCD=180°﹣（∠CBD+∠BDC）=180°﹣60°=120°， ∴∠ECD=∠CED=180°...

    查看答案和解析>>

    同步练习册答案