
如图, 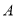 、
、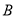 是双曲线上的两点,过
是双曲线上的两点,过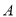 点作
点作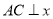 轴于点
轴于点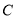 ,交
,交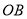 于点
于点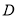 .若
.若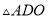 的面积为
的面积为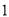 ,
, 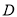 为
为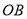 的中点,则
的中点,则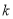 的值为__________.
的值为__________.

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源:2017-2018学年七年级数学人教版上册:第4章 几何图形初步 单元测试卷 题型:单选题
如图,∠AOB为平角,且∠AOC=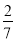 ∠BOC,则∠BOC的度数是( )
∠BOC,则∠BOC的度数是( )
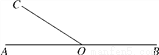
A. 140° B. 135° C. 120° D. 40°
A 【解析】设∠BOC=x°,根据∠AOC=∠BOC,则 , 为平角, , 计算得出: . 故选A.查看答案和解析>>
科目:初中数学 来源:云南省楚雄州2017-2018学年上学期期末教学质量监测九年级数学试卷 题型:解答题
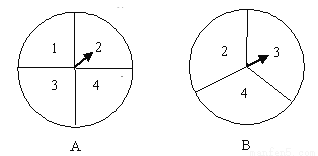
甲乙两人在玩转盘游戏时,把转盘A、B分别分成4等份、3等份,并在每一份内标上数字,如图所示.游戏规定:转动两个转盘停止后,指针必须指到某一数字,否则重转.
(1)请用树状图或列表法列出所有可能的结果;
(2)若指针所指的两个数字都是方程x2-5x+6=0的解时,则甲获胜;若指针所指的两个数字都不是方程x2-5x+6=0的解时,则乙获胜,问他们两人谁获胜的概率大?请分析说明.
查看答案和解析>>
科目:初中数学 来源:陕西省2018届九年级上学期期中考试数学试卷 题型:解答题
(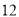 分)在菱形
分)在菱形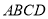 中,
中, 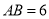 ,
, 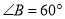 ,点
,点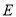 是线段
是线段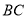 上的一个动点.
上的一个动点.
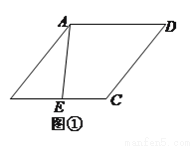
(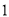 )如图①,求
)如图①,求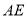 的最小值.
的最小值.
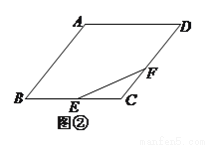
(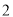 )如图②,若
)如图②,若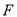 也是
也是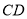 边上的一个动点,且
边上的一个动点,且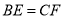 ,求
,求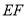 的最小值.
的最小值.
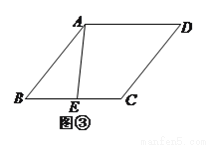
(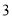 )如图③,若
)如图③,若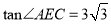 ,则在菱形内部存在一点
,则在菱形内部存在一点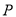 ,使得点
,使得点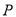 分别到点
分别到点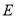 、点
、点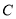 、边
、边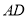 的距离之和最小.请你画出这样的点
的距离之和最小.请你画出这样的点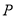 ,并求出这个最小值.
,并求出这个最小值.
查看答案和解析>>
科目:初中数学 来源:陕西省2018届九年级上学期期中考试数学试卷 题型:解答题
(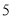 分)如图,一次函数
分)如图,一次函数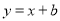 的图象与反比例函数
的图象与反比例函数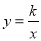 图象交于
图象交于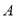 ,
, 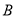 两点,点
两点,点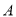 的坐标为
的坐标为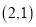 .
.
(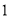 )求一次函数和反比例函数的表达式.
)求一次函数和反比例函数的表达式.
(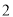 )求
)求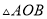 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源:陕西省2018届九年级上学期期中考试数学试卷 题型:单选题
将抛物线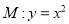 向右平移
向右平移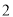 个单位,再向下平移
个单位,再向下平移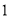 个单位,得到抛物线
个单位,得到抛物线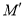 ,
, 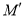 与
与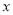 轴交于
轴交于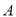 、
、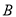 两点,
两点, 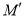 的顶点记为
的顶点记为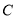 ,则
,则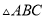 的面积为( ).
的面积为( ).

A. 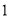 B.
B. 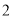 C.
C. 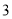 D.
D. 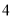
查看答案和解析>>
科目:初中数学 来源:人教版九年级年级数学下册第二十九章 达标检测卷 题型:单选题
小明在某天下午测量了学校旗杆的影子长度,按时间顺序排列正确的是( )
A. 6m,5m,4m B. 4m,5m,6m C. 4m,6m,5m D. 5m,6m,4m
B 【解析】下午太阳逐渐落下,旗杆的影子长度越来越长,所以按时间顺序,学校旗杆的影子长度可能为4m、5m、6m. 故答案选B.查看答案和解析>>
科目:初中数学 来源:人教版七年级下册数学第五章相交线与平行线单元检测卷 题型:填空题
两个角的两边分别平行,若其中一个角比另一个角的2倍少30°,则这两个角的度数分别为________.
70°,110°或30°,30° 【解析】(1)如图(1), 由题意知:AB//DE,BC//EF, 假设∠B为x°,则∠E=2x°-30°, ∵AB//DE, ∴∠1=∠B=x°, 又∠1=∠2,∴∠1=∠2=x°, 又∵BC//EF, ∴∠2+∠E=180°, ∴ ,解得x=70, ∴∠B=70°,∠E=2×70°-30°=110°. ...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com