
若AD是△ABC的中线,则下列结论中错误的是( )
A. AB=BC B. BD=DC C. AD平分BC D. BC=2DC
A 【解析】【解析】 ∵AD是△ABC的中线,∴AD平分BC ,∴BD=DC,BC=2DC.故A错误.故选A.科目:初中数学 来源:北师大版数学七年级下册第三章3.1用表格表示的变量间关系课时练习 题型:单选题
以21m/s的速度向上抛一个小球,小球的高度h(m)与小球运动的时间t(s)之间的关系是h=21t﹣4.9t2.下列说法正确的是( )
A. 4.9是常量,21,t,h是变量 B. 21,4.9是常量,t,h是变量
C. t,h是常量,21,4.9是变量 D. t,h是常量,4.9是变量
B 【解析】A.21是常量,故A错误; B.21,4.9是常量,t,h是变量,故B是正确; C、D.t、h是变量,21,4.9是常量,故C、D错误; 故选:B.查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下4.1.2 三角形的三边关系 同步练习 题型:单选题
下列长度的三根小木棒能构成三角形的是( )
A. 2 cm,3 cm,5 cm B. 7cm,4 cm,2 cm
C. 3 cm,4 cm,8 cm D. 3 cm,3 cm,4 cm
D 【解析】A选项:2+3=5,故不能构成三角形; B选项:4+2<7,故不能构成三角形; C选项:3+4<8,故不能构成三角形; D选项:3+3〉4,故能构成三角形. 故选D.查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下4.1.3 三角形的中线、角平分线 同步练习 题型:单选题
过△ABC的顶点A,作BC边上的高,以下作法正确的是( )
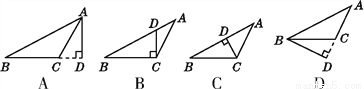
A. A B. B C. C D. D
A 【解析】【解析】 △ABC中BC边上的高正确的是A选项.故选A.查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下4.1.3 三角形的中线、角平分线 同步练习 题型:填空题
有一质地均匀的三角形铁片,若阿龙想用木棒撑住此铁片,则支撑点应设在该三角形的____处最恰当.
重心 【解析】【解析】 有一质地均匀的三角形铁片,若阿龙想用木棒撑住此铁片,则支撑点应设在该三角形的重心处最恰当.故答案为:重心.查看答案和解析>>
科目:初中数学 来源:北师大版七年级下册 第四章 三角形 4.5 利用三角形全等测距离 同步测试 题型:单选题
把等腰直角三角形的三角板按如图所示的方式立在桌面上,顶点A顶着桌面,若另两个顶点分别距离桌面5cm和3cm,则过另外两个顶点向桌面作垂线,则垂足之间的距离即DE的长为( )
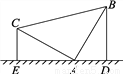
A. 4cm B. 6cm C. 8cm D. 求不出来
C 【解析】∵ ∠BAC=90° ∠AEC=90° ∴ ∠BAC=∠AEC ∵ ∠DAB+∠BAC=∠DAC ∠ECA+∠AEC=∠DAC ∠BAC=∠DEC ∴ ∠ECA=∠DAB ∵ △ABD是直角三角形 △CAE是直角三角形 AB=AC ∠ECA=∠DAB ∴ △ABD≌△CAE (一边一锐角对应相等的两个直角三角形全等) ∴ AE=BD AD=CE...查看答案和解析>>
科目:初中数学 来源:北师大版七年级下册 第四章 三角形 4.5 利用三角形全等测距离 同步测试 题型:单选题
利用三角形全等测量距离的原理是( )
A. 全等三角形对应角相等 B. 全等三角形对应边相等
C. 大小和形状相同的两个三角形全等 D. 三边对应相等的两个三角形全等
B 【解析】利用三角形全等测量距离,是指无法直接测量时,我们通过构造全等的方法,然后借助全等三角形对应边相等,间接测量距离,故选B.查看答案和解析>>
科目:初中数学 来源:内蒙古包头市青山区2017-2018学年八年级(上)期末数学试卷 题型:单选题
若kb>0,则函数y=kx+b的图象可能是( )
A. 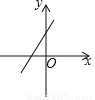 B.
B. 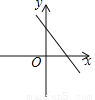 C.
C. 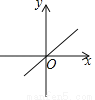 D.
D. 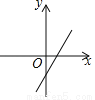
查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下5.3.1 等腰三角形的性质 同步练习 题型:单选题
如图,△ABC是等边三角形,AD是角平分线,△ADE是等边三角形,下列结论:①AD⊥BC;②EF=FD;③BE=BD.其中正确结论的个数为( )

A. 3 B. 2 C. 1 D. 0
A 【解析】试题解析:∵△ABC是等边三角形,AD是∠BAC的平分线, ∴AD⊥BC,BD=DC, ∴∠ADC=90°. 故① 正确. ∵△ABC和△ADE是等边三角形, ∴AE=AD,AB=AC,∠EAD=∠BAC=60°, ∴∠EAD-∠BAD=∠BAC-∠BAD, ∴∠BAE=∠DAC. 在△BAE和△CAD中,AE=AD,∠EAB=∠D...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com