
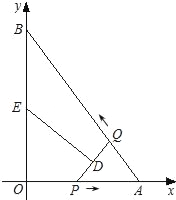
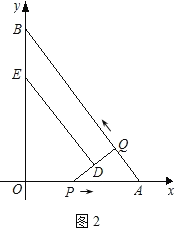
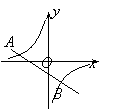
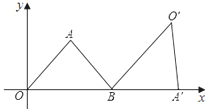
��ͼ����ƽ��ֱ������ϵxOy�У�ֱ��AB��x�ύ�ڵ�A����y�ύ�ڵ�B����OA=3��AB=5����P�ӵ�O������OA��ÿ��1����λ�����ٶ����A�����˶��������A��������ԭ�����ٶ���AO���أ���Q�ӵ�A������AB��ÿ��1����λ�����ٶ����B�����˶���������P��Q���˶���DE���ִ�ֱƽ��PQ���ҽ�PQ�ڵ�D��������QB��BO��OP�ڵ�E����P��Qͬʱ����������Q�����Bʱֹͣ�˶�����PҲ��ֹ֮ͣ�����P��Q�˶���ʱ����t�루t��0����
��1����ֱ��AB�Ľ���ʽ��
��2���ڵ�P��O��A�˶��Ĺ����У����APQ�����S��t֮��ĺ�����ϵʽ������д��t��ȡֵ��Χ����
��3���ڵ�E��B��O�˶��Ĺ����У�����������⣺
���ı���QBED�ܷ��Ϊֱ�����Σ����ܣ������t��ֵ�������ܣ���˵�����ɣ�
�ڵ�DE������Oʱ������ֱ��д��t��ֵ��
���𰸡���1��ֱ��AB�Ľ���ʽΪ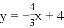 ����2��S=��
����2��S=�� t2+
t2+ t��
t��
��3���ı���QBED�ܳ�Ϊֱ�����Σ���t=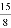 ���ڵ�DE������Oʱ��t=
���ڵ�DE������Oʱ��t= ��
��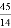 ��
��
����������������1����������Rt��AOB��,OA=3,AB=5,���OB��ֵ��Ȼ�����ô���ϵ�����������һ�κ����Ľ���ʽ��
��2������Q��QF��AO�ڵ�F.�ɡ�AQF�ס�ABO,�������������εĶ�Ӧ�߳ɱ����������ڷ��̼������QF�ij���Ȼ�����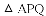
��3���ٷֱ��DE��QB��PQ��BOȥ���������������������ε����ʣ��������t��ֵ��
�ڸ��������֪��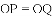
�������
(1)��Rt��AOB��,OA=3,AB=5,�ɹ��ɶ�����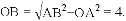
��A(3,0),B(0,4).
��ֱ��AB�Ľ���ʽΪy=kx+b.
��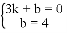 .���
.���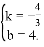
��ֱ��AB�Ľ���ʽΪ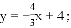
(2)��ͼ1������Q��QF��AO�ڵ�F.
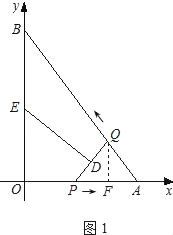
��AQ=OP=t����AP=3?t.
�ɡ�AQF�ס�ABO,��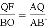
��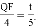
��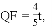
��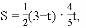
��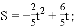
(3)�ı���QBED�ܳ�Ϊֱ������,
����ͼ2,��DE��QBʱ��
��DE��PQ��
��PQ��QB���ı���QBED��ֱ������.
��ʱ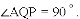
�ɡ�APQ�ס�ABO,��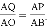
��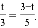
���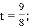
��ͼ3,��PQ��BOʱ��
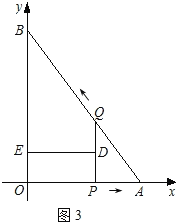
��DE��PQ��
��DE��BO���ı���QBED��ֱ������.
��ʱ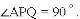
�ɡ�AQP�ס�ABO,��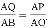
��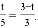
3t=5(3?t)��
3t=15?5t��
8t=15��
���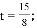
(��P��A��0�˶��Ĺ����л�������,������������ȥ).
�ڵ�DE������Oʱ��
��DE��ֱƽ��PQ��
��EP=EQ=t��
����P��Q��ͬ��ʱ����ٶȣ�
��AQ=EQ=EP=t��
���AEQ=��EAQ��
��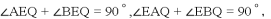
���BEQ=��EBQ��
��BQ=EQ��
��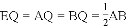
����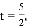
��P��A��O�˶�ʱ��
����Q��QF��OB��F��
EP=6?t,
��EQ=EP=6?t��
AQ=t��BQ=5?t��
��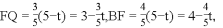
��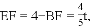
��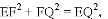
��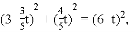
��ã�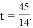
�൱DE������Oʱ, 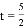 ��
��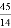 .
.
�㾦�����⿼��֪ʶ��϶࣬���ɶ���������ϵ������һ�κ�������ʽ�����������ε��ж������ʵ�֪ʶ�㣬�������պ����ø���֪ʶ���ǽ���Ĺؼ�.
�����͡������
��������
21
��ͼ������������y��(m��0)��һ�κ���y��kx��b(k��0)��ͼ���ཻ��A��B���㣬��A������Ϊ(��6��2)����B������Ϊ(3��n)������������һ�κ����Ľ���ʽ��

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2018��㶫ʡ�����н������п���ѧһģ�Ծ� ���ͣ���ѡ��
��ͼ�����������ͬ��С��������ɵļ����壬����������ͼ�ǣ�������
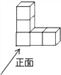
A.  B.
B.  C.
C. 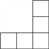 D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ������������2018����꼶�п�һģ�Ծ���ѧ�Ծ� ���ͣ���ѡ��
��ͼ����AOBΪ���������Σ�����A�����꣨2�� 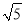 �����ױ�OB��x���ϣ�����AOB�Ƶ�B��˳ʱ�뷽����תһ���ǶȺ�á�A��O��B����A�Ķ�Ӧ��A����x���ϣ����O�������Ϊ��������
�����ױ�OB��x���ϣ�����AOB�Ƶ�B��˳ʱ�뷽����תһ���ǶȺ�á�A��O��B����A�Ķ�Ӧ��A����x���ϣ����O�������Ϊ��������
A. ��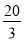 ��
�� 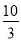 �� B. ��
�� B. ��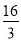 ��
�� 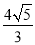 �� C. ��
�� C. ��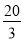 ��
�� 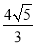 �� D. ��
�� D. ��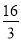 ��4
��4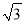 ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ������������2018����꼶�п�һģ�Ծ���ѧ�Ծ� ���ͣ���ѡ��
��x=��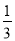 ��y=4�������ʽ3x+y��3��ֵΪ��������
��y=4�������ʽ3x+y��3��ֵΪ��������
A. ��6 B. 0 C. 2 D. 6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�Ƹ���2018����꼶�п�ȫ��ģ���Ծ���������ѧ�Ծ� ���ͣ������
�����x�IJ���ʽ�飺 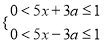 ������aΪ������
������a������
���𰸡�������
������������������������ʽ����ÿ������ʽ�Ľ⼯���ֱ������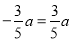 ʱ����
ʱ����
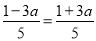 ʱ����
ʱ����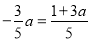 ʱ����
ʱ����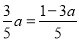 ʱa��ֵ����ϲ���ʽ�Ľ⼯����������ڸ��εIJ���ʽ��Ľ⼯��
ʱa��ֵ����ϲ���ʽ�Ľ⼯����������ڸ��εIJ���ʽ��Ľ⼯��
��������� 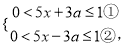
�ⲻ��ʽ�ٵã� 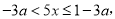
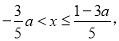
�ⲻ��ʽ�ڵã� 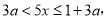
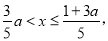
�ߵ�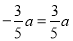 ʱ��a=0��
ʱ��a=0��
��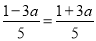 ʱ��a=0��
ʱ��a=0��
��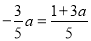 ʱ��
ʱ�� 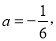
��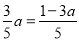 ʱ��
ʱ�� 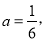
�൱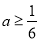 ��
��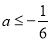 ʱ��ԭ����ʽ���⣻
ʱ��ԭ����ʽ���⣻
��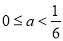 ʱ��ԭ����ʽ��Ľ⼯Ϊ
ʱ��ԭ����ʽ��Ľ⼯Ϊ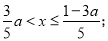
��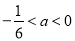 ʱ��ԭ����ʽ��Ľ⼯Ϊ��
ʱ��ԭ����ʽ��Ľ⼯Ϊ�� 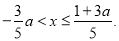
�����͡������
��������
16
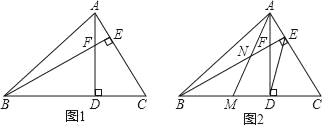
��ͼ1������ǡ�ABC�У���ABC=45�㣬����AD��BE�ཻ�ڵ�F��
��1���ж�BF��AC��������ϵ��˵�����ɣ�
��2����ͼ2������ACD���߶�AD���ۣ���C����BD�ϵĵ�M��AM��BE�ཻ�ڵ�N����DE��AMʱ���ж�NE��AC��������ϵ��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2018���п���ѧģ���Ծ����壩 ���ͣ������
��1�����㣺����2����1��|��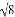 |+��
|+��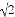 ��1��0+cos45�㣮
��1��0+cos45�㣮
��2����֪m2��5m��14=0����m��1����2m��1������m+1��2+1��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2018����꼶�п���ѧһģ�Ծ� ���ͣ���ѡ��
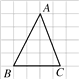
��ABC�������������е�λ����ͼ��ʾ����cosB��ֵΪ(����)
A. 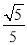 B.
B. 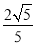 C.
C. 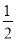 D. 2
D. 2
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com