
科目:初中数学 来源:山东省聊城市2018届九年级一模考试数学试卷 题型:解答题
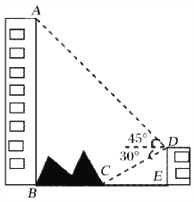
如图,大楼底右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上). 已知AB=80m,DE=10m,求障碍物B,C两点间的距离.(结果精确到0.1m)
(参考数据: 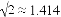 ,
,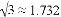 )
)
查看答案和解析>>
科目:初中数学 来源:江苏省苏州市2017届九年级中考数学预测试卷 题型:单选题
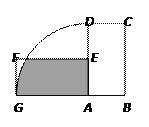
如图,将矩形ABCD绕点A逆时针旋转90°至矩形AEFG,点D的旋转路径为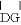 ,若AB=1,BC=2,则阴影部分的面积为( )
,若AB=1,BC=2,则阴影部分的面积为( )
A. 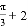 B.
B. 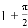 C.
C.  D.
D. 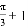
查看答案和解析>>
科目:初中数学 来源:2018年广东省阳江市江城区中考数学一模试卷 题型:单选题
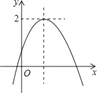
已知二次函数y=ax2+bx+c(a≠0)的图象如图,且关于x的一元二次方程ax2+bx+c﹣m=0没有实数根,有下列结论:
①b2﹣4ac>0;②abc<0;③m>2.
其中,正确结论的个数是( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源:山东省济宁市兖州市2018届九年级中考一模试卷数学试卷 题型:解答题
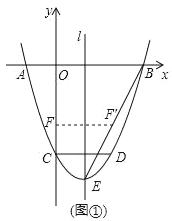
如图,二次函数y=x2+bx+c的图象与x轴交于 A、B两点,与y轴交于点C,OB=OC.点D在函数图象上,CD∥x轴,且CD=2,直线l是抛物线的对称轴,E是抛物线的顶点.
(1)求b、c的值;
(2)如图①,连接BE,线段OC上的点F关于直线l的对称点F'恰好在线段BE上,求点F的坐标;
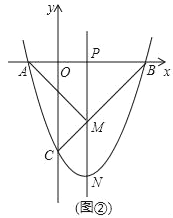
(3)如图②,动点P在线段OB上,过点P作x轴的垂线分别与BC交于点M,与抛物线交于点N.试问:抛物线上是否存在点Q,使得△PQN与△APM的面积相等,且线段NQ的长度最小?如果存在,求出点Q的坐标;如果不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源:山东省济宁市兖州市2018届九年级中考一模试卷数学试卷 题型:填空题
将从1开始的连续自然数按以下规律排列:
第1行 | 1 | ||||||||
第2行 | 2 | 3 | 4 | ||||||
第3行 | 9 | 8 | 7 | 6 | 5 | ||||
第4行 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | ||
第5行 | 25 | 24 | 23 | 22 | 21 | 20 | 19 | 18 | 17 |
…
则2018在第_____行.
查看答案和解析>>
科目:初中数学 来源:湖北省黄冈市2018届九年级中考全真模拟试卷(二)数学试卷 题型:解答题
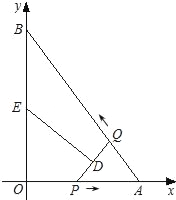
如图,在平面直角坐标系xOy中,直线AB与x轴交于点A,与y轴交于点B,且OA=3,AB=5.点P从点O出发沿OA以每秒1个单位长的速度向点A匀速运动,到达点A后立刻以原来的速度沿AO返回;点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动.伴随着P、Q的运动,DE保持垂直平分PQ,且交PQ于点D,交折线QB﹣BO﹣OP于点E.点P、Q同时出发,当点Q到达点B时停止运动,点P也随之停止.设点P、Q运动的时间是t秒(t>0).
(1)求直线AB的解析式;
(2)在点P从O向A运动的过程中,求△APQ的面积S与t之间的函数关系式(不必写出t的取值范围);
(3)在点E从B向O运动的过程中,完成下面问题:
①四边形QBED能否成为直角梯形?若能,请求出t的值;若不能,请说明理由;
②当DE经过点O时,请你直接写出t的值.
【答案】(1)直线AB的解析式为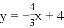 ;(2)S=﹣
;(2)S=﹣ t2+
t2+ t;
t;
(3)四边形QBED能成为直角梯形.①t=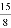 ;②当DE经过点O时,t=
;②当DE经过点O时,t= 或
或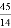 .
.
【解析】分析:(1)首先由在Rt△AOB中,OA=3,AB=5,求得OB的值,然后利用待定系数法即可求得一次函数的解析式;
(2)过点Q作QF⊥AO于点F.由△AQF∽△ABO,根据相似三角形的对应边成比例,借助于方程即可求得QF的长,然后即可求得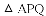
(3)①分别从DE∥QB与PQ∥BO去分析,借助于相似三角形的性质,即可求得t的值;
②根据题意可知即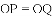
详【解析】
(1)在Rt△AOB中,OA=3,AB=5,由勾股定理得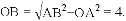
∴A(3,0),B(0,4).
设直线AB的解析式为y=kx+b.
∴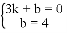 .解得
.解得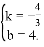
∴直线AB的解析式为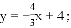
(2)如图1,过点Q作QF⊥AO于点F.
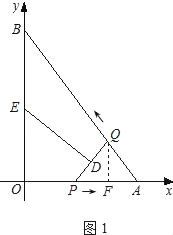
∵AQ=OP=t,∴AP=3?t.
由△AQF∽△ABO,得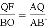
∴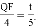
∴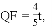
∴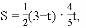
∴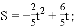
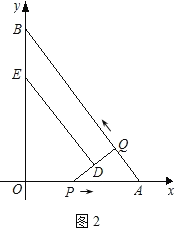
(3)四边形QBED能成为直角梯形,
①如图2,当DE∥QB时,
∵DE⊥PQ,
∴PQ⊥QB,四边形QBED是直角梯形.
此时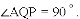
由△APQ∽△ABO,得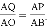
∴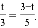
解得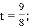
如图3,当PQ∥BO时,
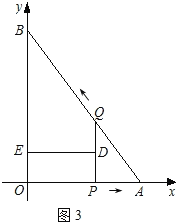
∵DE⊥PQ,
∴DE⊥BO,四边形QBED是直角梯形.
此时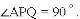
由△AQP∽△ABO,得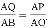
即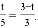
3t=5(3?t),
3t=15?5t,
8t=15,
解得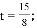
(当P从A向0运动的过程中还有两个,但不合题意舍去).
②当DE经过点O时,
∵DE垂直平分PQ,
∴EP=EQ=t,
由于P与Q相同的时间和速度,
∴AQ=EQ=EP=t,
∴∠AEQ=∠EAQ,
∵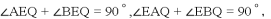
∴∠BEQ=∠EBQ,
∴BQ=EQ,
∴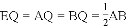
所以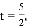
当P从A向O运动时,
过点Q作QF⊥OB于F,
EP=6?t,
即EQ=EP=6?t,
AQ=t,BQ=5?t,
∴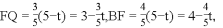
∴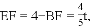
∵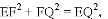
即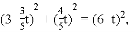
解得: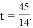
∴当DE经过点O时, 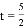 或
或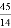 .
.
点睛:本题考查知识点较多,勾股定理,待定系数法求一次函数解析式,相似三角形的判定与性质等知识点,熟练掌握和运用各个知识点是解题的关键.
【题型】解答题
【结束】
21
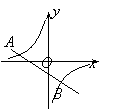
如图,反比例函数y=(m≠0)与一次函数y=kx+b(k≠0)的图象相交于A、B两点,点A的坐标为(-6,2),点B的坐标为(3,n).求反比例函数和一次函数的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com