
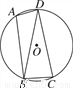
如图,已知四边形ABCD内接于圆O,连接BD,∠BAD=105°,∠DBC=75°.
(1)求证:BD=CD;
(2)若圆O的半径为3,求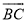 的长.
的长.
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案科目:初中数学 来源:北师大版 七年级数学下册 第一章 整式的乘除 单项式与单项式相乘 专题练习题 含答案 题型:填空题
若2amb3m+n与a2b2n的和仍是一个单项式,则2amb3m+n·a2b2n=_______.
2a4b24 【解析】试题分析:同类项是指所含字母相同,且相同字母的指数也相同的单项式.根据题意可得: ,解得: ,则原式=.查看答案和解析>>
科目:初中数学 来源:2017-2018学年九年级数学北师大版上册 全册综合测试卷2 题型:解答题
数学活动——探究特殊的平行四边形.
问题情境
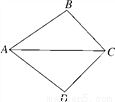
如图,在四边形ABCD中,AC为对角线,AB=AD,BC=DC.请你添加条件,使它们成为特殊的平行四边形.
提出问题
(1)第一小组添加的条件是“AB∥CD”,则四边形ABCD是菱形.请你证明;
(2)第二小组添加的条件是“∠B=90°,∠BCD=90°”,则四边形ABCD是正方形.请你证明.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年九年级数学北师大版上册 全册综合测试卷2 题型:单选题
一次函数y=ax-a与反比例函数y=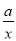 (a≠0)在同一平面直角坐标系中的图象可能是( )
(a≠0)在同一平面直角坐标系中的图象可能是( )
A. 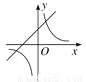 B.
B. 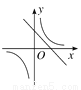 C.
C. 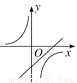 D.
D. 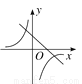
查看答案和解析>>
科目:初中数学 来源:江苏省苏州市张家港市2016-2017学年九年级(上)期末数学试卷 题型:解答题
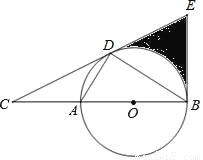
如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,CD=2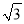 .
.
①若∠C=30°,求图中阴影部分的面积;
②若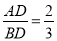 ,求BE的长.
,求BE的长.
查看答案和解析>>
科目:初中数学 来源:江苏省苏州市张家港市2016-2017学年九年级(上)期末数学试卷 题型:填空题
圆锥的母线长5cm,底面半径长3cm,那么它的侧面展开图的圆心角是 度.
216°. 【解析】 试题分析:易得圆锥的底面周长,也就是圆锥侧面展开图的弧长,利用弧长公式即可求得侧面展开图的圆心角. 试题解析:∵圆锥的底面半径长3cm, ∴圆锥的底面周长为6πcm, 设扇形的圆心角为n°, ∴, 解得n=216°.查看答案和解析>>
科目:初中数学 来源:江苏省苏州市张家港市2016-2017学年九年级(上)期末数学试卷 题型:单选题
若点M(﹣1,y1),N(1,y2),P(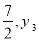 )都在抛物线y=﹣mx2+4mx+m2+1(m>0)上,则下列结论正确的是( )
)都在抛物线y=﹣mx2+4mx+m2+1(m>0)上,则下列结论正确的是( )
A. y1<y2<y3 B. y1<y3<y2 C. y3<y1<y2 D. 2<y1<y3
B 【解析】观察二次函数的图象可知:y1<y3<y2. 故选:B.查看答案和解析>>
科目:初中数学 来源:北师大版数学七年级下册第一章整式乘法1.7整式的除法课时练习 题型:填空题
(2a3b2+8a2c)÷2a2等于_______;
ab2+4c 【解析】(2a3b2+8a2c)÷2a2=2a3b2÷2a2+8a2c÷2a2= ab2+4c, 故答案为:ab2+4c.查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学人教版5.1相交线同步练习 题型:单选题
如图,直线AB,CD相交于点O,OA平分∠COE,∠COE=70°,则∠BOD的度数是( )
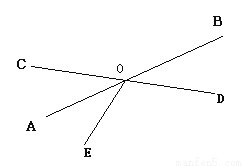
A. 20° B. 30° C. 35° D. 40°
C 【解析】首先利用相交线的性质确定对顶角相等,然后根据角平分线定义得出所求角与已知角的关系转化求解. 【解析】 ∵∠COE=70°且OA平分∠COE, ∴∠COA=∠COE=35°, 又∵∠COA与∠BOD是对顶角, ∴∠BOD = ∠COA =35°. 故选C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com