
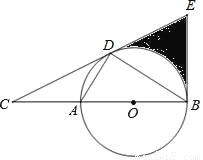
如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,CD=2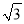 .
.
①若∠C=30°,求图中阴影部分的面积;
②若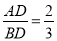 ,求BE的长.
,求BE的长.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:北师大版七年级数学下2.3.1 平行线的性质 同步练习 题型:单选题
如图,AB∥ CD,∠ A=50°,则∠ 1的大小是( )
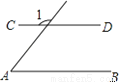
A. 50° B. 120° C. 130° D. 150°
C 【解析】试题分析:如图,∵AB∥CD,∴∠A+∠3=180°,∴∠3=130°,∴∠1=∠3=130°.故选C.查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下册 第一章 整式的乘除 整式的运算 专题练习题 含答案 题型:解答题
计算:3xy2·(-2xy)
-6x2y3 【解析】试题分析:同底数幂的乘法法则,底数不变,指数相加.将系数相乘,然后根据同底数幂的乘法法则得出答案. 试题解析:原式=-6x2y3.查看答案和解析>>
科目:初中数学 来源:2017-2018学年九年级数学北师大版上册 全册综合测试卷2 题型:单选题
已知△ABC∽△A′B′C′,△A′B′C′的面积为6cm2,周长为△ABC周长的一半,则△ABC的面积等于( )
A. 1.5cm2 B. 3cm2 C. 12cm2 D. 24cm2
D 【解析】根据题意求出两个三角形的周长比,即可得出相似比,然后根据相似三角形的性质解答即可. 【解析】 ∵△ABC与△A′B′C′的周长比为2:1,且△ABC∽△A′B′C′, ∴△ABC与△A′B′C′的面积比为4:1,又△A′B′C′的面积为6 cm2, ∴△ABC的面积=24 cm2, 故选:D.查看答案和解析>>
科目:初中数学 来源:2017-2018学年九年级数学北师大版上册 全册综合测试卷2 题型:单选题
若A(3,y1),B(2,y2)在函数y=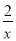 的图象上,则y1,y2的大小关系是( )
的图象上,则y1,y2的大小关系是( )
A. y1>y2 B. y1=y2 C. y1<y2 D. 无法确定
C 【解析】试题分析:把点A(3, ),B(2, )代入反比例函数得,3×=2,2×=2,解得=, =1,所以<.故选C.查看答案和解析>>
科目:初中数学 来源:江苏省苏州市张家港市2016-2017学年九年级(上)期末数学试卷 题型:解答题
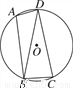
如图,已知四边形ABCD内接于圆O,连接BD,∠BAD=105°,∠DBC=75°.
(1)求证:BD=CD;
(2)若圆O的半径为3,求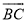 的长.
的长.
查看答案和解析>>
科目:初中数学 来源:江苏省苏州市张家港市2016-2017学年九年级(上)期末数学试卷 题型:填空题
已知m是方程3x2﹣6x﹣2=0的一根,则m2﹣2m=_____.
【解析】把x=m代入方程得:3m2﹣6m﹣2=0, 即3m2﹣6m=2,3(m2﹣2m)=2, ∴m2﹣2m=, 故答案是: .查看答案和解析>>
科目:初中数学 来源:北师大版数学七年级下册第一章整式乘法1.7整式的除法课时练习 题型:解答题
(-6 x4 y7)÷ (-2 x y2) ÷(-3 x2y4)
- x y 【解析】试题分析:由单项式除以单项式法则与同底数幂的除法法则可完成此题 试题解析:(-6 x4 y7)÷ (-2 x y2) ÷(-3 x2y4)= - x4-1-2y7-2-4=- xy.查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学人教版5.1相交线同步练习 题型:填空题
如图所示,其中共有________对对顶角.
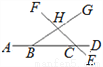
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com