练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    正六边形的边长为4cm，它的边心距等于__________cm；

    【解析】如图所示，AB=4cm，过O作OG⊥AB于G， ∵此多边形是正六边形， ∴∠AOB==60°，∠AOG==30°， ∴OG=AGtan∠AOG == ， 故答案为： ．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：江苏省扬州市2016-2017学年八年级上学期期末考试数学试卷 题型：单选题

    在平面直角坐标系中，直线与x轴、y轴分别交于A、B两点，点O为坐标原点，若在该坐标平面内有以点P（不与点A、B、O重合）为顶点的直角三角形与Rt△ABO全等，且这个以点P为顶点的直角三角形与Rt△ABO有一条公共边，则所有符合条件的P点个数为（　　）

    A. 9个 B. 7个 C. 5个 D. 3个

    B 【解析】【解析】 如图，图中的P1、P2、P3、P4、P5、P6、P7，就是符合要求的点P，注意以P1为公共点的直角三角形有3个．故选B．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年八年级数学下册（华师大版）：期末检测1 题型：填空题

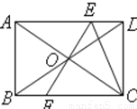
    如图，矩形ABCD的周长为20cm，两条对角线相交于O点，过点O作AC的垂线EF，分别交AD、BC于E、F点，连结CE，则△CDE的周长为 cm.

    10 【解析】 试题分析：根据矩形的性质结合EF是AC的垂线，可得AE=CE，即可得到结果。 ∵矩形ABCD的周长为20cm， ∴AD+DC=10cm， ∵矩形ABCD， ∴AO=CO， ∵EF是AC的垂线， ∴AE=CE， ∴CE+DE+CD=AE+DE+CD= AD+DC=10cm， ∴△CDE的周长为10cm.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年八年级数学下册（华师大版）：期末检测1 题型：单选题

    在端午节到来之前，学校食堂推荐了A、B、C三家粽子专卖店，对全校师生爱吃哪家店的粽子作调查，以决定最终向哪家店采购，下面统计量中最值得关注的是( )

    A. 平均数 B. 众数 C. 中位数 D. 方差

    B 【解析】试题解析：由于众数是数据中出现次数最多的数，故学校食堂最值得关注的应该是统计调查数据的众数． 故选B．

    查看答案和解析>>

    科目：初中数学 来源：广东省2018届九年级上学期学业检测（二）数学试卷 题型：解答题

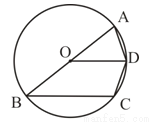
    已知：如图，C，D是以AB为直径的⊙O上的两点，且OD∥BC．求证：AD=DC。

    见解析证明． 【解析】 试题分析：连结OC，根据平行线的性质得到∠1=∠B，∠2=∠3，而∠B=∠3，所以可得∠1=∠2，根据圆心角、弧、弦的关系即可得到结论． 试题解析：连结OC，如图，∵OD∥BC，∴∠1=∠B，∠2=∠3，又∵OB=OC，∴∠B=∠3，∴∠1=∠2，∴AD=DC．

    查看答案和解析>>

    科目：初中数学 来源：广东省2018届九年级上学期学业检测（二）数学试卷 题型：单选题

    若关于x的一元二次方程（k﹣1）x2+2x﹣2=0有两个不相等的实数根，则k的取值范围是（　　）

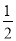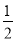    A. k＞ B. k≥ C. k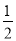＞且k≠1 D. k≥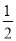且k≠1

    C 【解析】试题分析：根据题意得k-1≠0且△=2²-4（k-1）×（-2）＞0，解得：k＞且k≠1．故选C

    查看答案和解析>>

    科目：初中数学 来源：广东省2018届九年级上学期学业检测（二）数学试卷 题型：单选题

    方程x2－2x＝0的根是( )

    A. x1＝x2＝0 B. x1＝x2＝2 C. x1＝0，x2＝2 D. x1＝0，x2＝－2

    C 【解析】根据因式分解法解一元二次方程的方法，提取公因式x可得x（x-2）=0，然后按照ab=0的形式的方程解法，可得x=0或x-2=0，解得x1＝0，x2＝2. 故选：C.

    查看答案和解析>>

    科目：初中数学 来源：湖北省孝感市八校联谊2017-2018学年九年级上册数学12月联考试卷 题型：单选题

    如图，某小区计划在一块长为32m，宽为20m的矩形空地上修建三条同样宽的道路，剩余的空地上种植草坪，使草坪的面积为570m2 ．若设道路的宽为 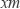，则下面所列方程正确的是（   ）

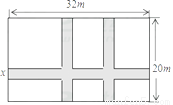
    A. (32-x)(20-x)=32×20-570                        B. 32x+2×20x=32×20-570

    C. 32x+2×20x-2x2=570 D. (32-2x)(20-x)= 570

    D 【解析】通过平移可将六块草坪拼为一块，可得一个大矩形，由图易得该矩形的长为(32?2x)m,宽为（20-x）m，由此根据题意可得： ( 32 ? 2 x ) ( 20 ? x ) = 570. 故选D.

    查看答案和解析>>

    科目：初中数学 来源：北京市海淀区2017-2018学年八年级上学期期末考试数学试卷 题型：解答题

    如图，A，B，C，D是同一条直线上的点，AC=BD，AE∥DF，∠1=∠2．求证：BE = CF．

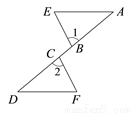
    证明见解析 【解析】试题分析：由AC=BD，AE∥DF可得AB=DC，∠A=∠D，再根据∠1=∠2利用ASA证明△ABE≌△DCF即可得. 试题解析：∵AC=AB+BC，BD=BC+CD，AC=BD， ∴AB=DC， ∵AE∥DF， ∴∠A=∠D， 在△ABE和△DCF中， ， ∴△ABE≌△DCF， ∴BE=CF．

    查看答案和解析>>

    同步练习册答案