
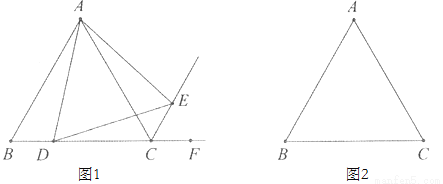
�����߶���ȵ������ν����ȱ������Σ����������Ƕ���60��. ��ABC�ǵȱ������Σ���D��BC����ֱ�����˶�������AD����AD����ֱ�ߵ��Ҳ�����DAE=60�㣬����ABC����ǡ�ACF�Ľ�ƽ��������ֱ���ڵ�E.
��1����ͼ1������D���߶�BC��ʱ���������AD��AE�Ĵ�С��ϵ��������֤����
��2����ͼ2������D���߶�BC�ķ����ӳ�����ʱ���������ⲹȫͼ�Σ������������ۻ�������?��˵������.

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�������н�����2017����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
�ⷽ�̣�
��1�� 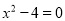 ��
��
��2��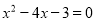 .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ�����ѧ���꼶�ϲ����в��� ���ͣ���ѡ��
����4����: 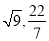 ,��,(
,��,( 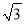 )0,������������(��)
)0,������������(��)
A. 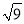 B.
B. 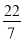 C. �� D. (
C. �� D. (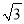 )0
)0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ�����2017-2018ѧ����꼶��ѧ�����п�����ѧ�Ծ�. ���ͣ���ѡ��
��ͼ����֪�ڡ�ABC��AB��AC�����Ե�BΪԲ�ģ�BC��Ϊ�뾶����������AC�ڵ�E�������н���һ����ȷ���ǣ�������
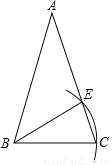
A. AE��EC B. AE��BE C. ��EBC����BAC D. ��EBC����ABE
C �������������������AB=AC�����ABC=��ACB�����Ե�BΪԲ�ģ�BC��Ϊ�뾶����������AC�ڵ�E����BE=BC�����ACB=��BEC�����BEC=��ABC=��ACB�����A=��EBC����ѡC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ�����2017-2018ѧ����꼶��ѧ�����п�����ѧ�Ծ�. ���ͣ���ѡ��
����˵����ȷ���ǣ�������
A. ȫ����������ָ��״��ͬ��С��ȵ�������
B. ȫ����������ָ�����ȵ�������
C. �ܳ���ȵ���������ȫ��������
D. ���еĵȱ������ζ���ȫ��������
A �����������������A����״��ͬ��С��ȵ��������ܹ���ȫ�غϣ���ȫ�������Σ��ʱ�ѡ����ȷ�� B�������ȵ���������״��һ����ͬ�����Բ�һ����ȫ�غϣ��ʱ�ѡ����� C���ܳ���ȵ������Σ���״��һ����ͬ����С��һ����ȣ����Բ�һ����ȫ�������Σ��ʱ�ѡ����� D�����еĵȱ���������״����ͬ����С��߳��йأ��߳�����ȣ����ܹ��غϣ����Բ�һ����ȫ�������Σ��ʱ�ѡ����� ��ѡA�� ...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����������2017-2018ѧ����ѧ�ڳ��а��꼶���п�����ѧ�Ծ� ���ͣ������
��ͼ����A��C��B��D��ͬһ��ֱ���ϣ�BE��DF����A=��F��AB=FD����֤��AE=FC.
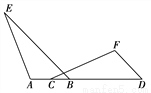
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����������2017-2018ѧ����ѧ�ڳ��а��꼶���п�����ѧ�Ծ� ���ͣ������
��ͼ��AC=DC��BC=EC����������һ���ʵ���������______________��ʹ�á�ABC�ա�DEC��
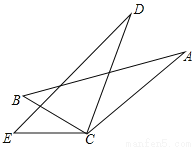
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ2018����꼶����ĩģ����ѧ�Ծ� ���ͣ������
������������κ����Ľ���ʽ��
��1�������ߵĶ�������Ϊ����1����1��������y�ύ���������Ϊ��3
��2����������x���Ͻصõ��߶γ�Ϊ4���Ҷ��������ǣ�3����2����
��1��y=��2x2��4x��3����2��y=x2��3x+ �����������������Ӧ�ô���ϵ���������ÿ�����κ����Ľ���ʽ���Ƕ��ټ��ɣ� �����������1���������ߵĶ�������Ϊ����1����1���� ���������ߵĽ���ʽΪ��y=a��x+1��2��1�� ����������y�ύ���������Ϊ��3�� �ੁ3=a��0+1��2��1�� ���a=��2�� �������ߵĽ���ʽ��y=��2��x+1��2��1�� ...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������б������ڶ���2018����꼶12���¿���ѧ�Ծ� ���ͣ���ѡ��
������x��һԪ���η���ax2+x��1=0��ʵ��������a��ȡֵ��Χ�ǣ�������
A. a��-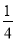 ��a��0 B. a��-
��a��0 B. a��-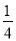 C. a��-
C. a��-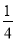 D. a��-
D. a��-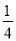 ��a��0
��a��0
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com