练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

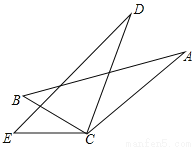
    如图，AC=DC，BC=EC，请你添加一个适当的条件：______________，使得△ABC≌△DEC．

    CE=BC．本题答案不唯一． 【解析】添加条件是：AB=DE， 在△ABC与△DEC中, ， ∴△ABC≌△DEC. 故答案为：CE=BC. 本题答案不唯一.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：重庆市江津区2017届九年级下学期期末考试数学试卷 题型：单选题

    如图，将直角三角板60°角的顶点放在圆心O上，斜边和一直角边分别与⊙O相交于A、B两点，P是优弧AB上任意一点（与A、B不重合），则∠APB＝（　 　 ）

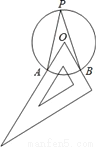
    A. 30° B. 45° C. 50° D. 60°

    A 【解析】试题解析：由题意得，∠AOB=60°， 则∠APB=∠AOB=30°． 故选A．

    查看答案和解析>>

    科目：初中数学 来源：山东省无棣县2017-2018学年八年级上学期期中考试数学试卷. 题型：填空题

    计算: ___________.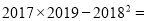

    -1 【解析】2017×2019-2018² =(2018-1)(2018+1)-2018² =2018²-1²-2018² =-1 故答案为:-1.

    查看答案和解析>>

    科目：初中数学 来源：北京四中2017-2018学年上学期初中八年级期中考试数学试卷 题型：解答题

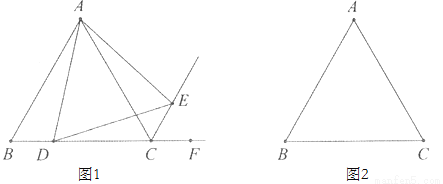
    三条边都相等的三角形叫做等边三角形，它的三个角都是60°. △ABC是等边三角形，点D在BC所在直线上运动，连接AD，在AD所在直线的右侧作∠DAE=60°，交△ABC的外角∠ACF的角平分线所在直线于点E.

    （1）如图1，当点D在线段BC上时，请你猜想AD与AE的大小关系，并给出证明；

    （2）如图2，当点D在线段BC的反向延长线上时，依据题意补全图形，请问上述结论还成立吗?请说明理由.

    （1）AD=AE,证明见解析；（2）成立，证明见解析. 【解析】试题分析: （1）由等边三角形的性质得到∠B=∠ACE=60°，AB=AC，再有∠DAB=∠EAC可证明△ABD≌△ACE即可得到结论； （2）由等边三角形的性质得到∠ABD=∠ACE=120°，AB=AC，再有∠DAB=∠EAC可证明△ABD≌△ACE即可得到结论. 试题解析: （1）结论：AD=AE，理由如...

    查看答案和解析>>

    科目：初中数学 来源：北京四中2017-2018学年上学期初中八年级期中考试数学试卷 题型：解答题

    先化简（1-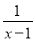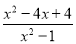）÷，再选一个适当的数代入求值.

    ，选取的值不能是±l，2 【解析】先通分再计算，然后将分母不为0的值代入即可．

    查看答案和解析>>

    科目：初中数学 来源：北京四中2017-2018学年上学期初中八年级期中考试数学试卷 题型：单选题

    如图，D为∠BAC的外角平分线上一点并且满足BD=CD，∠DBC=∠DCB，过D作DE⊥AC于E，DF⊥AB交BA的延长线于F，则下列结论：

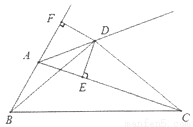
    ①△CDE≌△BDF；②CE=AB+AE；③∠BDC=∠BAC；④∠DAF=∠CBD.

    其中正确的结论有（ ）.

    A. 1个 B. 2个 C. 3个 D. 4个

    D 【解析】∵AD平分∠CAF，DE⊥AC，DF⊥AB， ∴DE=DF， 在Rt△CDE和Rt△BDF中， ， ∴Rt△CDE≌Rt△BDF(HL)，故①正确； ∴CE=AF， 在Rt△ADE和Rt△ADF中， ， ∴Rt△ADE≌Rt△ADF(HL)， ∴AE=AF， ∴CE=AB+AF=AB+AE，故②正确； ∵Rt△CD...

    查看答案和解析>>

    科目：初中数学 来源：北京四中2017-2018学年上学期初中八年级期中考试数学试卷 题型：单选题

    在平面直角坐标系中，点A，点B关于y轴对称，点A的坐标是（2，-8），则点B的坐标是（ ）.

    A. （-2，-8） B. （2，8） C. （-2，8） D. （8，2）

    A 【解析】试题解析：根据关于轴的对称点的坐标特点：横坐标互为相反数，纵坐标不变. ∵点A,点B关于y轴对称,点A的坐标是(2,?8)， ∴点B的坐标是(?2,?8)， 故选：A.

    查看答案和解析>>

    科目：初中数学 来源：山西省2018届九年级上期末模拟数学试卷 题型：填空题

    方程2x﹣x2=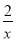的正实数根有________ 个

    0 【解析】试题解析：在同一坐标系中，分别作出y1=2x-x2与y2=的图象如下： 由图象可以看出，正实数根有0个．

    查看答案和解析>>

    科目：初中数学 来源：山东省临沂市费县2017-2018学年八年级（上）期中数学试卷 题型：填空题

    如图，在△PAB中，PA=PB，M，N，K分别是PA，PB，AB上的点，且AM=BK，BN=AK，若∠MKN=44°，则∠P的度数为　 　．

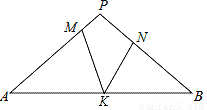
    92° 【解析】【解析】 ∵PA=PB，∴∠A=∠B，在△AMK和△BKN中，∵AM=BK，∠A=∠B，AK=BN，∴△AMK≌△BKN，∴∠AKM=∠BNK，∵∠AKN=∠B+∠BNK，即∠AKM+∠MKN=∠B+∠BNK，∴∠B=∠MKN=44°，∴∠P=180°﹣2×44°=92°．故答案为：92°．

    查看答案和解析>>

    同步练习册答案