
���塱��jiong���������������һ���������Ƶ����飮��ͼ��ʾ��һ�ű߳�Ϊ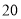 �������ε�ֽƬ����ȥ����һ����Сֱ�������κ�һ�������εõ�һ�����塱��ͼ������Ӱ���֣������ȥ��С�����γ��Ϳ��ֱ���
�������ε�ֽƬ����ȥ����һ����Сֱ�������κ�һ�������εõ�һ�����塱��ͼ������Ӱ���֣������ȥ��С�����γ��Ϳ��ֱ���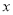 ��
��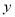 ����ȥ������Сֱ�������ε���ֱ�DZ߳�Ҳ�ֱ�Ϊ
����ȥ������Сֱ�������ε���ֱ�DZ߳�Ҳ�ֱ�Ϊ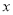 ��
�� 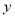 ��
��
��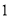 ���ú���
���ú���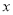 ��
��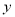 �Ĵ���ʽ��ʾͼ�С��塱����Ӱ���֣��������
�Ĵ���ʽ��ʾͼ�С��塱����Ӱ���֣��������
��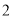 ����
����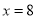 ��
�� 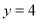 ʱ�����ʱ���塱�������
ʱ�����ʱ���塱�������

 99��1������ĩ��ѵ��ϵ�д�
99��1������ĩ��ѵ��ϵ�д� ��ǿ��У��ĩ���100��ϵ�д�
��ǿ��У��ĩ���100��ϵ�д� �óɼ�1��1��ĩ���100��ϵ�д�
�óɼ�1��1��ĩ���100��ϵ�д� ��״Ԫ���źþ�ϵ�д�
��״Ԫ���źþ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡƽ���������2017-2018ѧ��ȵ�һѧ����ĩ��ѧ�Ծ����� ���ͣ������
��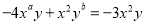 ����b-a= ��
����b-a= ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���Ĵ�ʡ������2017-2018ѧ����꼶��ѧ���ϣ���ĩģ���Ծ� ���ͣ���ѡ��
���е���̨��̨�꣬�����ĶԳ�ͼ�ε��ǣ� ��
A.  B.
B.  C.
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������2018��2017��������ĩ��̾� ���ͣ���ѡ��
��AΪ˫����y=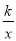 ��k��0����һ�㣬BΪx����һ�㣬�ҡ�AOBΪ�ȱ������Σ���AOB�ı߳�Ϊ2����k��ֵΪ��������
��k��0����һ�㣬BΪx����һ�㣬�ҡ�AOBΪ�ȱ������Σ���AOB�ı߳�Ϊ2����k��ֵΪ��������
A. 2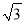 B. ��2
B. ��2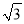 C.
C. 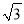 D. ��
D. ��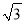
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������2018��2017��������ĩ��̾� ���ͣ���ѡ��
�ѷ���x��x+2��=5����һ��ʽ����a��b��c��ֵ�ֱ��ǣ�������
A. 1��2����5 B. 1��2����10 C. 1��2��5 D. 1��3��2
A ��������������������������ã�x2+2x-5=0�� ��a��b��c��ֵ�ֱ���1��2��-5�� ��ѡA�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ�꽭��ʡ�����г�һ��������ѧ�Ծ���ѧ�Ծ� ���ͣ������
���㣺 ��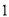 ��
��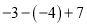 ����
����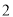 ��
��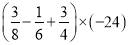 ��
��
��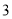 ��
��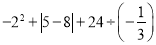 ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ�꽭��ʡ�����г�һ��������ѧ�Ծ���ѧ�Ծ� ���ͣ���ѡ��
��ͼ��Բ���ܳ�Ϊ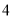 ����λ������Բ��
����λ������Բ��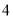 �ȷֵ㴦�ֱ����
�ȷֵ㴦�ֱ����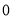 ��
��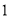 ��
��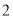 ��
��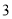 ������Բ���ϱ�ʾ����
������Բ���ϱ�ʾ����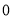 �ĵ��������ϱ�ʾ
�ĵ��������ϱ�ʾ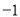 �ĵ��غϣ��ٽ����ᰴ��ʱ�뷽�����ڸ�Բ�ϣ���Բ���ϱ�ʾ����
�ĵ��غϣ��ٽ����ᰴ��ʱ�뷽�����ڸ�Բ�ϣ���Բ���ϱ�ʾ����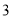 �ĵ��������ϱ�ʾ
�ĵ��������ϱ�ʾ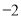 �ĵ��غ�
�ĵ��غ� �����λ��ƣ��������ϱ�ʾ
�����λ��ƣ��������ϱ�ʾ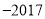 �ĵ���Բ�����غϵ������ǣ� ����
�ĵ���Բ�����غϵ������ǣ� ����
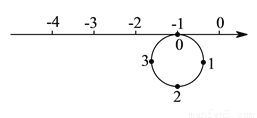
A. 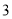 B.
B. 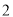 C.
C. 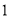 D.
D. 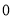
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㶫ʡ������Խ����2016-2017ѧ����꼶�²���ѧ��ĩ�����Ծ� ���ͣ������
��ͼ���ڡ�ABC�У�AD��BC��AB=5��BD=4��CD=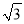 ��
��
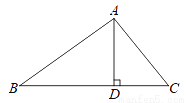
��1����AD�ij���
��2�����ABC���ܳ���
��1��3����2���� �������������������1����Rt��ABD�У����ݹ��ɶ��������AD�ij��� ��2����Rt��ACD�У����ݹ��ɶ��������AC�ij���Ȼ�������������ε��ܳ��������߳���֮����⼴��. �����������1����Rt��ABD�У�AD==3�� ��2����Rt��ACD�У�AC==2�� ���ABC���ܳ�=AB+AC+BC=5+4++2=9+3.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ����꼶��ѧ�²ᣨ��ʦ��棩�����м���� ���ͣ������
��ͼ����OΪ�ȱ�������ABC��һ�㣬����OA��OB��OC����OBΪһ������OBM��60�㣬��BO��BM������CM��OM.
(1)�ж�AO��CM�Ĵ�С��ϵ��֤����
(2)��OA��8��OC��6��OB��10���жϡ�OMC����״��֤����
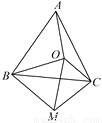
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com