
先化简(1﹣ )÷
)÷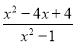 ,再从0,﹣2,﹣1,1中选择一个合适的数代入并求值.
,再从0,﹣2,﹣1,1中选择一个合适的数代入并求值.
科目:初中数学 来源:福建省2016-2017学年八年级下学期期末考试数学试卷 题型:单选题
如图,点P是矩形ABCD的边AD上的一动点,矩形的两条边AB、BC的长分别是6和8,则点P到矩形的两条对角线AC和BD的距离之和是( )
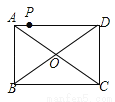
A.4.8 B.5 C.6 D.7.2
A. 【解析】 试题分析:连接OP,∵矩形的两条边AB、BC的长分别为6和8,∴S矩形ABCD=AB•BC=48,OA=OC,OB=OD,AC=BD=10,∴OA=OD=5,∴S△ACD=S矩形ABCD=24,∴S△AOD=S△ACD=12,∵S△AOD=S△AOP+S△DOP=OA•PE+OD•PF =×5×PE+×5×PF=(PE+PF)=12,解得:PE+PF=4.8.故选...查看答案和解析>>
科目:初中数学 来源:北京市西城外国语学校2017-2018学年度第一学期八年级数学期中试卷 题型:解答题
解分式方程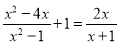
查看答案和解析>>
科目:初中数学 来源:北京市西城外国语学校2017-2018学年度第一学期八年级数学期中试卷 题型:单选题
如图,B,D,E,C四点共线,且△ABD≌△ACE,若∠AEC=105°,则∠DAE的度数等于( ).

A. 30° B. 40° C. 50° D. 65°
A 【解析】【解析】 ∵△ABD≌△ACE,∴∠ADB=∠AEC=105°,∴∠ADE=∠AED=75°,∴∠DAE=180°﹣75°﹣75°=30°,故选A.查看答案和解析>>
科目:初中数学 来源:黑龙江省大庆市2016---2017学年度上期初三数学期末试卷 题型:解答题
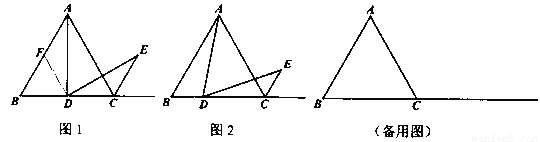
(10分)(1)【问题发现】小明遇到这样一个问题:
如图1,△ABC是等边三角形,点D为BC的中点,且满足∠ADE=60°,DE交等边三角形外角平分线CE所在直线于点E,试探究AD与DE的数量关系.
(1)小明发现,过点D作DF//AC,交AC于点F,通过构造全等三角形,经过推理论证,能够使问题得到解决,请直接写出AD与DE的数量关系: ;
(2)【类比探究】如图2,当点D是线段BC上(除B,C外)任意一点时(其它条件
不变),试猜想AD与DE之间的数量关系,并证明你的结论.
(3)【拓展应用】当点D在线段BC的延长线上,且满足CD=BC(其它条件不变)时,
请直接写出△ABC与△ADE的面积之比.
查看答案和解析>>
科目:初中数学 来源:黑龙江省大庆市2016---2017学年度上期初三数学期末试卷 题型:填空题
如图,在ΔABC中,∠ABC=120°,点D、E分别在AC和AB上,且AE=ED=DB=BC,则∠A的度数为______°.
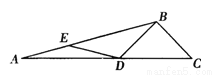
查看答案和解析>>
科目:初中数学 来源:黑龙江省大庆市2016---2017学年度上期初三数学期末试卷 题型:填空题
平行四边形的一个内角平分线将该平行四边形的一边分为2cm和3cm两部分,则该平行四边形的周长为 .
14cm或16cm 【解析】 试题分析:根据题意画出图形,由平行四边形得出对边平行,又由角平分线可以得出△ABE为等腰三角形,然后分别讨论BE=2cm,CE=3cm或BE=3cm,CE=2cm,继而求得答案. 【解析】 如图,∵四边形ABCD为平行四边形, ∴AD∥BC, ∴∠DAE=∠AEB, ∵AE为角平分线, ∴∠DAE=∠BAE, ∴∠AE...查看答案和解析>>
科目:初中数学 来源:浙江省余姚市2017-2018学年八年级上学期期中考试数学试卷 题型:解答题
已知:如图,直线AD与BC交于点O,OA=OD,OB=OC.求证:AB∥CD.
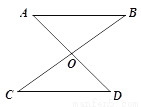
查看答案和解析>>
科目:初中数学 来源:南京市玄武区2016~2017学年度第一学期期九年级试卷 题型:单选题
抛掷一枚质地均匀的骰子一次,向上一面点数大于4的概率是( )
A. 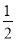 B.
B. 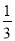 C.
C. 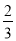 D.
D. 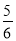
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com