
���������У������ж�������ȫ�ȵ��ǣ� ��
A. �����߶�Ӧ��� B. ���ߺ�һ�Ƕ�Ӧ���
C. ���Ǻ�����һ�ǵĶԱ߶�Ӧ��� D. ���Ǻ����ǵļб߶�Ӧ���
B ��������Ҫ�����ѡ�������֤�����ݸ���ѡ�����֪�������������ȫ�ȵ��ж����������ж�������B����SSAʱ�����ж�������ȫ�ȵģ�����ѡB�� �������� A�������߶�Ӧ��ȵ���������ȫ�������Σ�����SSS�� B�����ߺ�һ�Ƕ�Ӧ��ȵ������β�һ����ȫ�������Σ� C�����Ǻ�����һ�ǵĶԱ߶�Ӧ�����ȫ�������Σ�����AAS�� D�����Ǻ����ǵļб߶�Ӧ�����ȫ�������Σ�����ASA�� ��ѡ...
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡ2016-2017ѧ����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
���㣺 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���Ϻ��л�����2018����꼶��ѧ����ĩ���в�����ѧ�Ծ���WORD�棩 ���ͣ���ѡ��
��֪���κ���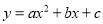 ��ͼ�������ͼ��ʾ�������й�ϵʽ�г������ǣ� ��
��ͼ�������ͼ��ʾ�������й�ϵʽ�г������ǣ� ��
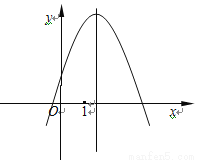
A. 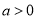 B.
B. 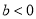 C.
C. 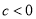 D.
D. 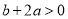 ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�����������������ѧУ2017-2018ѧ��ȵ�һѧ�ڰ��꼶��ѧ�����Ծ� ���ͣ������
�������ʽ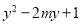 ����ȫƽ��ʽ����ô
����ȫƽ��ʽ����ô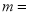 ________
________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�����������������ѧУ2017-2018ѧ��ȵ�һѧ�ڰ��꼶��ѧ�����Ծ� ���ͣ���ѡ��
��ͼ, С��ͬѧ��ѧϰ��ȫ�������ε����֪ʶ����, ֻ��������ȫ��ͬ�ij�����ֱ�߾Ϳ�������һ���ǵ�ƽ����. ��ͼ: һ��ֱ��ѹס����OB, ��һ��ֱ��ѹס����OA�������һ��ֱ�߽��ڵ�P, С��˵: ������OP���ǡ�BOA�Ľ�ƽ���ߡ�. ����������������(�� ) .
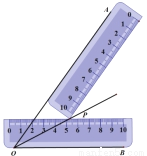
A. ��ƽ�����ϵĵ㵽��������ߵľ������
B. �ǵ��ڲ����ǵ����ߵľ�����ȵĵ��ڽǵ�ƽ������
C. ������������ƽ���ߵĽ��㵽�����ߵľ������
D. ���Ͼ�����ȷ
B �������������������ȫ��ͬ�ij��ӣ��ȿ�����P���ǵ����߾����dz��ӿ��ȣ�����OP�ǽ�ƽ���ߣ��������õ��ǽǵ��ڲ����ǵ����ߵľ�����ȵĵ��ڽǵ�ƽ������.��ѡB.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������ʡ������2016---2017ѧ������ڳ�����ѧ��ĩ�Ծ� ���ͣ������
�ڡ�ABC�У���B+��ACB=30�㣬AB=4����ABC��ʱ����תһ���ǶȺ����ADE�غϣ��ҵ�Cǡ�ó�ΪAD�е㣬��ͼ
��1��ָ����ת���ģ��������ת�ǵĶ�����
��2�������BAE�Ķ�����AE�ij���
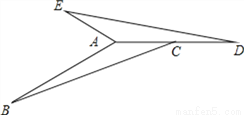
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������ʡ������2016---2017ѧ������ڳ�����ѧ��ĩ�Ծ� ���ͣ������
��2a=3b=4c����abc��0����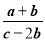 ��ֵ�� ______ ��
��ֵ�� ______ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������ʡ������2016---2017ѧ������ڳ�����ѧ��ĩ�Ծ� ���ͣ���ѡ��
��������ʽ�Т�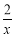 ����
����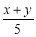 ����
����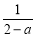 ����
����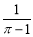 �з�ʽ�У� ������
�з�ʽ�У� ������
A��1�� B�� 2�� C��3�� D��4��
B�� �������� ������������ݷ�ʽ�Ķ��壬��ĸ�к�����ĸ��ʽ���Т٣��ۣ��������еķ�ʽ�������� ��ѡ��B���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���Ͼ���������2016~2017ѧ��ȵ�һѧ���ھ��꼶�Ծ� ���ͣ������
�ڶ��κ���y��ax2��bx��c�У�y��x�IJ��ֶ�Ӧֵ���±���

��m��n�Ĵ�С��ϵΪ m_______n�����������������������
�� ���������������� �ɱ���֪��ͼ��Գ���Ϊֱ��x������m, n�ֱ�Ϊ�㣨1��m���ͣ�2��n���������꣬�������ֱ��x=�Գƣ���m=n,�ʴ�Ϊ��=.�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com