
��ͼ����ABC����ƽ�Ƶ���DEFλ�ã����ǵ��ص����ֵ�����ǡ�ABC��һ�룬��BC=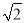 ����BE= ��
����BE= ��
���𰸡�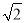 -1.
-1.
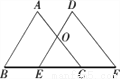
���������������֪��OE��AB��
���OEC�ס�ABC��
��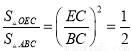 ����
����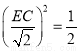 ����ã�EC=1.
����ã�EC=1.
��BE=BC-EC=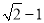 .
.
�����͡������
��������
14
���ε��ܳ�Ϊ16�����ڽǶ����ı�Ϊ1:2�������ε����Ϊ .
8 . ����������ͼ���������֪��������ABCD�У���A+��ADC=180�㣬��A����ADC=1:2��AD=AB=�� ���A=60�㣬 ����D��DE��AB�ڵ�E�����DEA=90�㣬 ���ADE=30�㣬 ��AE=AD=2�� ��DE=, ��S����ABCD=ABDE=.
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ���㶫ʡ���������ѧУ2017-2018ѧ����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ������
��ͼ����ƽ��ֱ������ϵ�У���֪��A(-2��0),B(0,3)��O Ϊԭ�㣮
��1���������� AOB �������
(2)���߶� AB �� x ������ƽ��4����λ�����߶�A��B�䣬x������һ��C����������A��B��C�����Ϊ 9 �����C�����꣮
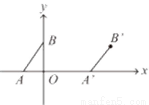
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰���꼶�ϲ���ѧ 23.1ͼ�ε���ת��1������ ���ͣ���ѡ��
��ͼ����Rt��ABC�У���ACB=90�㣬��A=30�㣬BC=2������ABC�Ƶ�C˳ʱ�뷽����ת60���õ���EDC����ʱ��D��б��AB�ϣ�б��DE��AC�ڵ�F����ͼ����Ӱ���ֵ����Ϊ��������
A. 2 B. 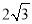 C.
C. 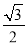 D.
D. 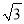
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ����ˮ��2018����꼶��ѧ�ڵڶ����¿���ѧ�Ծ� ���ͣ������
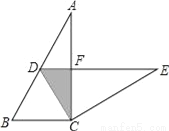
��ͼ��������ABCD�У�MΪBC��һ�㣬F��AM���е㣬EF��AM������ΪF����AD���ӳ����ڵ�E����DC�ڵ�N��
��1����֤����ABM �ס�EFA��
��2����AB=12��BM=5����DE�ij���
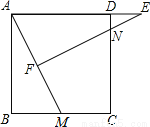
���𰸡���1��֤������������2��4.9.
�������������������1���������ε����ʵó�AB=AD����B=90�㣬AD��BC���ó���AMB=��EAF�����ɡ�B=��AFE�����ɵó����ۣ�
��2���ɹ��ɶ������AM���ó�AF���ɡ�ABM�ס�EFA�ó�����ʽ�����AE�����ɵó�DE�ij���
�����������1�����ı���ABCD�������Σ�
��AB=AD����B=90�㣬AD��BC��
���AMB=��EAF��
�֡�EF��AM��
���AFE=90�㣬
���B=��AFE��
���ABM�ס�EFA��
��2���ߡ�B=90�㣬AB=12��BM=5��
��AM=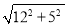 =13��AD=12��
=13��AD=12��
��F��AM���е㣬
��AF=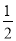 AM=6.5��
AM=6.5��
�ߡ�ABM�ס�EFA��
��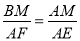 ��
��
��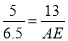 ��
��
��AE=16.9��
��DE=AE-AD=4.9��
���㣺1.���������ε��ж������ʣ�2.�����ε����ʣ�
�����͡������
��������
26
��ͼ������ABCD�У�AB=16cm��BC=6cm����P�ӵ�A������AB���B�ƶ��������A��B�غϣ���һֱ�����BΪֹ��ͬʱ����Q�ӵ�C������CD���D�ƶ��������C��D�غϣ����˶�ʱ����Ϊt�룮
��1������P��Q����3cm/s���ٶ��ƶ�����AP=����cm��QC=����cm�����ú�t�Ĵ���ʽ��ʾ��
��2������PΪ3cm/s���ٶ��ƶ�����Q��2cm/s���ٶ��ƶ��������ʱ��PD=PQ��ʹ��DPQΪ���������Σ�
��3������P��Q����3cm/s���ٶ��ƶ��������ʱ�䣬�ı���BPDQΪ���Σ�
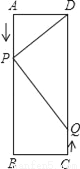
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ����ˮ��2018����꼶��ѧ�ڵڶ����¿���ѧ�Ծ� ���ͣ������
��ͼ���� ABCD�У�EΪ�߶�AD��һ�㣬AE=4ED��CE��BD���ڵ�F����DF=4cm����BF�ij�Ϊ������������
ABCD�У�EΪ�߶�AD��һ�㣬AE=4ED��CE��BD���ڵ�F����DF=4cm����BF�ij�Ϊ������������
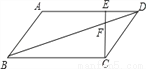
���𰸡�20
�����������ı���ABCD��ƽ���ı��Σ�AE=4ED��
��BC=AD=AE+ED=5ED��AD��BC��
���DEF�ס�BCF��
��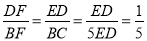 ����
����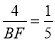 ��
��
��BF=20.
�����͡������
��������
19
�ⷽ�̣�(1) 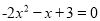 �� ��2��
�� ��2��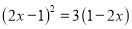 .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ����ˮ��2018����꼶��ѧ�ڵڶ����¿���ѧ�Ծ� ���ͣ���ѡ��
һ��������ֻװ��1�������2��������Щ�����ɫ�������ͬ���������һ�����Żز����ȣ����������һ�������������������Ǻ���ĸ����ǣ�������
A. 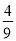 B.
B. 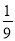 C.
C. 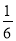 D.
D. 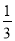
���𰸡�B
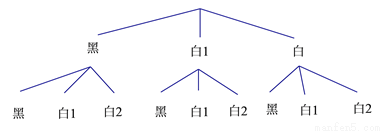
����������������ͼ���£�
��ͼ��֪������9�ֵȿ����¼����֣��������ζ��Ǻ���ռ����һ�֣�
��P�����������Ķ��Ǻ���=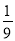 .
.
��ѡB.
�����͡���ѡ��
��������
9
��ͼ��A��B���ر�����������С��ͨ�����з��������A��B��ľ��룺����AB��ѡһ��C��Ȼ����AC��BC���е�M��N����������MN�ij�Ϊ12 m���ɴ�����֪����A��B��ľ��룬�й������̽����������������(����)
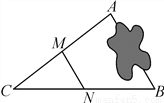
A. AB=24 m B. MN��AB C. ��CMN�ס�CAB D. CM��MA=1��2
D ��������������������������ε���λ��ƽ���ڵ����߲��ҵ��ڵ����ߵ�һ��ɵ�MN��AB��MN=AB���ٸ������������ε��ж���� �����������M��N�ֱ���AC��BC���е� ��MN��AB��MN=AB�� ��AB=2MN=2��12=24m ��CMN�ס�CAB ��M��AC���е� ��CM=MA ��CM��MA=1��1 �������������Dѡ� ��ѡD��...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ����ˮ��2018����꼶��ѧ�ڵڶ����¿���ѧ�Ծ� ���ͣ���ѡ��
����ʽ����ȷ����( )
A. 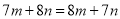 B.
B. 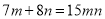
C. 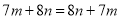 D.
D. 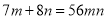
���𰸡�C
��������Aѡ���У� 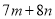 ��һ������
��һ������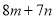 �����Ա�ѡ�����
�����Ա�ѡ�����
Bѡ���У� 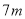 ��
��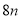 ����ͬ������ܺϲ������Ա�ѡ�����
����ͬ������ܺϲ������Ա�ѡ�����
Cѡ���У����ݼӷ��Ľ����ɣ� 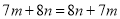 �����Ա�ѡ����ȷ��
�����Ա�ѡ����ȷ��
Dѡ���У� 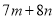 ����
����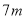 ��
��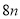 �ĺͣ�������
�ĺͣ�������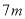 ��
��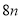 �Ļ������Ա�ѡ�����
�Ļ������Ա�ѡ�����
��ѡC.
�����͡���ѡ��
��������
2
���̣�x+1����x��2��=0�Ľ��ǣ����� ��
A. x=2 B. x=3 C. x1=��1��x2=3 D .x1=��1��x2=2
D ���������ߣ� ��� ���ã� . ��ѡD.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰���꼶�ϲ���ѧ ��25��С���븴ϰ ���� ���ͣ������
��֪����x��һԪ���η���x2��bx��c��0.�ӣ�1��2��3����������ȡһ��������Ϊ������b��ֵ���ٴ�ʣ�µ�����������ȡһ������Ϊ������c��ֵ����ʹ��һԪ���η�����ʵ�����ĸ�����________��
������������״ͼΪ�� �� ����6�ֵȿ��ܵĽ������ ��Ϊb2?4c?0�� ������ʹ��һԪ���η�����ʵ����ռ3�֣� b=2��c=?1�� b=3��c=?1�� b=3��c=2�� ������ʹ��һԪ���η�����ʵ�����ĸ���==. �ʴ�Ϊ�� .�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�Ϸ�����У2018����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ���ѡ��
��ͼ���ڡ�ABC�У���B=90�㣬AB=8��BC=4������ABC�۵���ʹ��A�Ķ�Ӧ��A������BC���ϣ��ۺ�ΪDE����AD�ij�Ϊy��A��B�ij�Ϊx����ôy��x֮��Ĺ�ϵͼ���Լ�ǣ�������
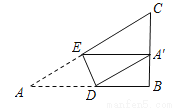
A. 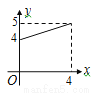 B.
B. 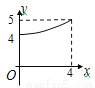
C. 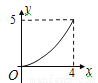 D.
D. 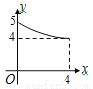
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com