
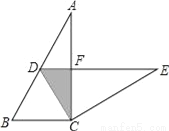
��ͼ����Rt��ABC�У���ACB=90�㣬��A=30�㣬BC=2������ABC�Ƶ�C˳ʱ�뷽����ת60���õ���EDC����ʱ��D��б��AB�ϣ�б��DE��AC�ڵ�F����ͼ����Ӱ���ֵ����Ϊ��������
A. 2 B. 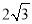 C.
C. 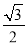 D.
D. 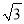

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ���˽̰���꼶�ϲ���ѧ 22.1.4���κ���yax2+bx+c��ͼ������ʣ�1������ ���ͣ���ѡ��
��ƽ��ֱ������ϵ�У�����������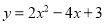 ������ƽ��3����λ���ȣ�������ƽ��2����λ���ȣ���������ƽ�ƺ����õ��������ߵĶ�������Ϊ�� ��
������ƽ��3����λ���ȣ�������ƽ��2����λ���ȣ���������ƽ�ƺ����õ��������ߵĶ�������Ϊ�� ��
A. ��-2,3�� B. ��-1,4�� C. ��1,4�� D. ��4,3��
D ������������ƽ�ơ� ���������ƽ�Ʊ仯�Ĺ��ɣ�����ƽ��ֻ�ı��ĺ����꣬����Ҽӡ�����ƽ��ֻ�ı��������꣬�¼��ϼӡ���ˣ���������y=2x2 - 4x+3������ƽ��3����λ���ȣ�������ƽ��2����λ���ȣ��䶥��Ҳͬ���任�� �ߵĶ��������ǣ�1��1���� ��㣨1��1��������ƽ��3����λ���ȣ�������ƽ��2����λ���ȣ��õ㣨4��3����������������ƽ�ƺ����������ߵĶ��������ǣ�...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㶫ʡ���������ѧУ2017-2018ѧ����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ���ѡ��
��ͼ��������ĵ�λ�����߶�Ϊ����һ�������Σ��Ա�ʾ��1�ĵ�ΪԲ�ģ������ζԽ��߳�Ϊ�뾶�������������ڵ�A�����A��ʾ�����ǣ� ��
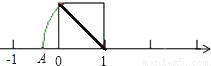
A. ��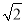 B. ��1+
B. ��1+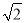 C. ��1��
C. ��1��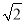 D. 1��
D. 1��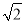
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰���꼶�ϲ���ѧ 23.1ͼ�ε���ת��1������ ���ͣ������
��ͼ������ABC������һ������˳ʱ��������תn��1��n��2��n��3���õ��������κ͡�ABC�ĶԳƹ�ϵ���� ����
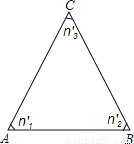
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰���꼶�ϲ���ѧ 23.1ͼ�ε���ת��1������ ���ͣ������
��ͼ����ABC�͡�A��B��C��������ȫ�غϵ�ֱ�����ǰ壬��B=30�㣬б�߳�Ϊ10cm�����ǰ�A��B��C��ֱ�Ƕ���C˳ʱ����ת������A������AB����ʱ��CA����ת�����ɵ����εĻ���Ϊ______cm��
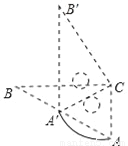
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰���꼶�ϲ���ѧ��13��13.3�����������Ρ� ���ͣ������
����������һ���ϵ����߰���������ε��ܳ��ֳ�15�M��12�M������������εĵױ߳�Ϊ______�M��
7��11 �����������������������Ϊ��ABC��AB��AC������BC�ǵױ�;BD��AC�ϵ����ߣ���ͼ�� ����������� ��AB+AD =15 CD+BC =12 ��AD=CD=AC=AB ��AB+AB =15 ��AB=10 ��10��+BC =12 ��BC=7 ��10+7=17��17 ����Թ��������Σ�����������֮�ʹ��ڵ����ߣ� ���ʱ���ױ߳�Ϊ7cm ��AB+AD =...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰���꼶�ϲ���ѧ��13��13.3�����������Ρ� ���ͣ���ѡ��
�����жϲ���ȷ����( )��
A. ����������������
B. ����������������
C. �ȱ������ε������ڽǶ���60��
D. �����ڽǷֱ�Ϊ120�㡢40����������ǵ���������
D �����������ݵ��������ε����ʣ����������ε�������ȣ�������ȣ����ݵȱ������ε����ʣ������ڽǶ���ȣ�������60�㣬���������ε��ڽǺ�Ϊ180�㣬��֪�����ڽǷֱ�Ϊ120�㣬40��������εĵ�������Ϊ20�㣬���ǵ���������. ��ѡ��D.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ����ˮ��2018����꼶��ѧ�ڵڶ����¿���ѧ�Ծ� ���ͣ������
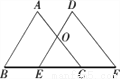
��ͼ����ABC����ƽ�Ƶ���DEFλ�ã����ǵ��ص����ֵ�����ǡ�ABC��һ�룬��BC=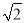 ����BE= ��
����BE= ��
���𰸡�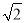 -1.
-1.
���������������֪��OE��AB��
���OEC�ס�ABC��
��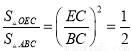 ����
����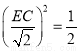 ����ã�EC=1.
����ã�EC=1.
��BE=BC-EC=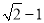 .
.
�����͡������
��������
14
���ε��ܳ�Ϊ16�����ڽǶ����ı�Ϊ1:2�������ε����Ϊ .
8 . ����������ͼ���������֪��������ABCD�У���A+��ADC=180�㣬��A����ADC=1:2��AD=AB=�� ���A=60�㣬 ����D��DE��AB�ڵ�E�����DEA=90�㣬 ���ADE=30�㣬 ��AE=AD=2�� ��DE=, ��S����ABCD=ABDE=.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����һ��ѧ��һѧ��5.2.3ȥ��ĸ��һԪһ�η��� ͬ����ϰ ���ͣ������
�ⷽ�̣�6��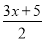 =
=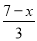 ��
��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com