
在平面直角坐标系中,线段OP的两个端点坐标分别为O(0,0),P(4, 3),将线段OP绕点O逆时针旋转90°到OP′位置,则点P′的坐标是( )

A.(3,4) B.(-4,3) C.(-3,4) D.(4,-3)
C. 【解析】 试题分析:如图,OA=3,PA=4, 把线段OP绕点O逆时针旋转90°到OP′位置可得OA旋转到x轴负半轴OA′的位置,OB旋转到y轴正半轴OB′的位置,所以P′A′=PA=4,P′B′=PB=3,即可得P′点的坐标为(﹣3,4).故答案选C.科目:初中数学 来源:江苏省徐州市丰县2018届九年级上学期第二次月考数学试卷 题型:单选题
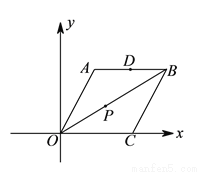
如图,菱形OABC在平面直角坐标系的位置如图所示,点B的坐标为(9,3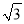 ),点D是AB的中点,点P在OB上,则△ADP的周长最小值为( )
),点D是AB的中点,点P在OB上,则△ADP的周长最小值为( )
A. 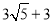 B.
B. 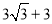 C.
C. 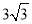 D.
D. 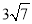
查看答案和解析>>
科目:初中数学 来源:2016-2017学年陕西省七年级(下)第二次测验数学试卷 题型:填空题
纽约与北京的时差为﹣13h,李伯伯在北京乘坐中午十二点的航班飞行约20h到达纽约,那么李伯伯到达纽约时间是_____点.
19 【解析】根据纽约与北京的时差为﹣13h,可列式求解为:12+20﹣13=32﹣13=19,所以李伯伯到达纽约时间是19点,即晚上7点. 故答案为:19.查看答案和解析>>
科目:初中数学 来源:江苏省徐州市丰县2017-2018学年八年级上学期第二次月考数学试卷 题型:解答题
如图,已知坐标系中点A(2,-1),B(7,-1),C(3,-3).
(1)判定△ABC的形状;
(2)设△ABC关于x轴的对称图形是△A1B1C1,若把△A1B1C1的各顶点的横坐标都加2.纵坐标不变,则△A1B1C1的位置发生什么变化?若最终位置是△A2B2C2,求C2点的坐标;
(3)试问在x轴上是否存在一点P,使PC-PB最大,若存在,求出PC-PB的最大值及P点坐标;若不存在,说明理由.
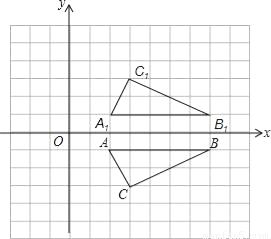
查看答案和解析>>
科目:初中数学 来源:江苏省徐州市丰县2017-2018学年八年级上学期第二次月考数学试卷 题型:填空题
如图,在数轴上点A和点B表示的数之间的整数是__________

查看答案和解析>>
科目:初中数学 来源:安徽省16-17学年度第一学期七年级数学期末考试卷 题型:解答题
如图1,一个棱长为1cm的正方体按某种方式展开后,恰好能放在一个长方形内.
(1)计算:图1长方形的面积S=_____________;
(2)小明认为把该正方体按某种方式展开后可以放在如图2所示的长方形内,请你在图2中画出这个正方体的平面展开图.
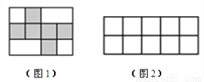
查看答案和解析>>
科目:初中数学 来源:安徽省16-17学年度第一学期七年级数学期末考试卷 题型:填空题
若5xm+1y5与3x2y2n+1是同类项,则m=________,n=________.
1 2 【解析】根据同类项的定义,得出关于m,n的方程,求出m,n的值. 【解析】 ∵单项式5xm+1y5与3x2y2n+1是同类项, ∴m+1=2,m=1,2n+1=5, n=2, 故答案为:1,2. “点睛”本题考查了同类项的知识,解答本题的关键是掌握同类项定义中的两个“相同”:相同字母的指数相同.查看答案和解析>>
科目:初中数学 来源:山西农业大学附属中学2017-2018学年八年级上学期第三次月考数学试卷 题型:解答题
通过学习,同学们已经体会到灵活运用乘法公式给整式的乘法运算带来的方便、快捷.相信通过下面材料的学习、探究,会使你大开眼界,并获得成功的喜悦.
例:用简便方法计算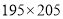 .
.
【解析】
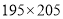
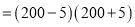 ①
①
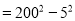 ②
②
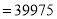 .
.
(1)例题求解过程中,第②步变形是利用 (填乘法公式的名称)
(2)用简便方法计算: 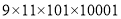 .
.
查看答案和解析>>
科目:初中数学 来源:黑龙江省哈尔滨市香坊区2017年中考数学二模试卷(解析版) 题型:单选题
已知点A(2,y1)、B(4,y2)都在反比例函数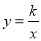 (k<0)的图象上,则y1、y2的大小关系为( )
(k<0)的图象上,则y1、y2的大小关系为( )
A. y1>y2 B. y1<y2 C. y1=y2 D. 无法确定
【答案】B
【解析】试题分析:∵当k<0时,y=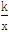 在每个象限内,y随x的增大而增大,∴y1<y2,故选B.
在每个象限内,y随x的增大而增大,∴y1<y2,故选B.
考点:反比例函数增减性.
【题型】单选题
【结束】
5
如图是由6个相同的小正方体搭成的几何体,那么这个几何体的俯视图是( )
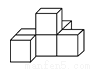
A. 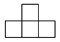 B.
B. 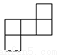 C.
C. 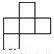 D.
D. 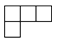
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com