
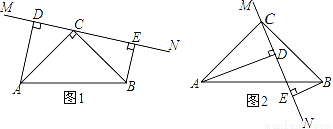
在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图1的位置时,求证:DE=AD+BE;
(2)当直线MN绕点C旋转到图2的位置时,(1)中的结论还成立吗?若成立,请给出证明;若不成立,请写出新的结论并说明理由.
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题八年级浙教版数学试卷(A卷) 题型:解答题
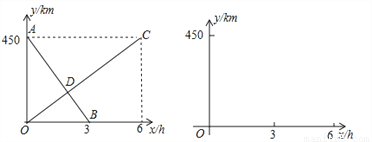
一列快车由甲地开往乙地,一列慢车由乙地开往甲地,两车同时出发, 匀速运动. 快车离乙地的路程y1(km) 与行驶的时间x(h) 之间的函数关系, 如图中线段AB 所示;慢车离乙地的路程y2(km) 与行驶的时间x(h)之间的函数关系, 如图中线段OC 所示。根据图象下列问题:
(1) 甲、乙两地之间的距离为__________km ;
(2) 线段AB 的解析式为_______________________;线段OC 的解析式为_________________________;
(3) 设快、慢车之间的距离为y(km), 求y 与慢车行驶时间x(h) 的函数关系式, 并画出函数的图象。
查看答案和解析>>
科目:初中数学 来源:浙江杭州拱墅区文澜中学2017-2018学年七年级上学期中考试数学试卷(含解析) 题型:单选题
若两数之和为负数,则下列叙述正确的是( ).
A. 两个都是负数 B. 这两个数不可能有正数
C. 两个数不可能有 D. 至少有一个负数
D. 至少有一个负数
查看答案和解析>>
科目:初中数学 来源:2017年四川省中考数学模拟试卷(3) 题型:填空题
若x1=﹣1是关于x的方程x2+mx﹣5=0的一个根,则方程的另一个根x2=__.
5 【解析】试题分析:首先将x=-1代入方程求出m的值,然后再去解关于x的一元二次方程.查看答案和解析>>
科目:初中数学 来源:2017年四川省中考数学模拟试卷(3) 题型:单选题
关于x的一元二次方程ax2﹣x+1=0有实数根,则a的取值范围是( )
A. a≤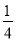 且a≠0 B. a≤
且a≠0 B. a≤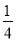 C. a≥
C. a≥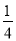 且a≠0 D. a≥
且a≠0 D. a≥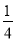
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题八年级人教版数学试卷(C卷) 题型:解答题
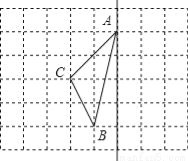
如图,在8×6正方形方格中,点A、B、C在小正方形的顶点上.
(1)在图中画出与△ABC关于直线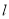 成轴对称的△AB′C′,并回答问题:
成轴对称的△AB′C′,并回答问题:
图中线段CC′被直线l ;
(2)在直线l上找一点D,使线段DB+DC最短.(不写作法,应保留作图痕迹)
(3) 在直线l确定一点P,使得|PA-PB|的值最小.(不写作法,应保留作图痕迹)
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题八年级人教版数学试卷(C卷) 题型:填空题
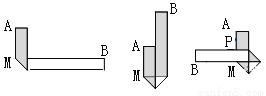
如图,一根长为30cm、宽为3 cm的长方形纸条,将它按图所示的过程折叠,为了美观,希望折叠完成后的纸条A端到点P的距离等于B端到点M的距离,则最初折叠时,MA的长应为__________cm.
查看答案和解析>>
科目:初中数学 来源:黄金30题系列 九年级数学 小题易丢分 题型:填空题
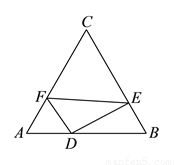
如图,在等边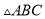 中,
中, 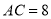 ,点
,点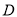 、
、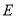 、
、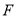 分别在三边
分别在三边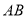 、
、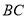 、
、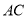 上,且
上,且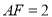 ,
, 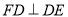 ,
, 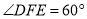 ,则
,则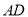 的长为__________.
的长为__________.
查看答案和解析>>
科目:初中数学 来源:甘肃省武威市2017-2018学年八年级(上)期中数学试卷 题型:单选题
如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处.若∠A=22°,则∠BDC等于( )
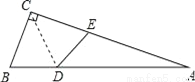
A. 44° B. 60° C. 67° D. 77°
C 【解析】试题分析:由∠ACB=90°,∠A=22°,三角形内角和是180º,可得∠B=90º-22º=68º,因为折叠角相等,所以∠CED=∠B=68º,∠BDC=∠EDC=∠BDE,,因为四边形内角和是360º,所以∠BDE=360º-90º-68º-68º=134º,所以∠BDC=∠BDE=×134º=67º.故选C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com