
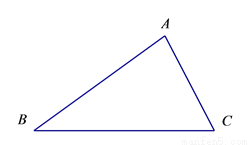
尺规作图:如图,已知△ABC.
求作△A1B1C1,使A1B1=AB,∠B1=∠B,B1C1=BC.
(作图要求:不写作法,不证明,保留作图痕迹)
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:北师大版七年级数学下册同步要点3.2 用关系式表示的变量间关系 题型:填空题
已知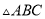 是等腰三角形,周长是
是等腰三角形,周长是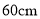 ,腰长为
,腰长为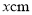 ,底为
,底为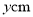 .
.
( )用含
)用含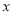 的关系式表示
的关系式表示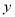 :__________.
:__________.
(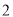 )当腰长由
)当腰长由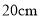 变化到
变化到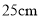 时,底边长由__________
时,底边长由__________ 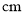 变化到__________
变化到__________ 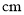 .
.
查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下4.3.3 用“边角边”判定三角形全等 同步练习 题型:解答题
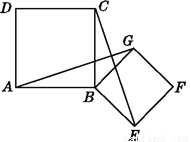
如图,四边形ABCD,四边形BEFG均为正方形,连接AG,CE.试说明:
(1)AG=CE;
(2)AG⊥CE.
查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下3.3 用图象表示的变量间关系 同步练习 题型:单选题
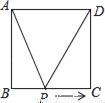
如图,正方形ABCD的边长为2cm,动点P从点A出发,在正方形的边上沿A→B→C的方向运动到点C停止,设点P的运动路程为x(cm)在下列图象中,表示△ADP的面积y(cm2)关于x(cm)的函数关系的图象是( )
A. 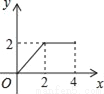 B.
B. 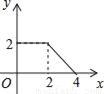 C.
C. 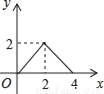 D.
D. 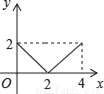
查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下3.3 用图象表示的变量间关系 同步练习 题型:单选题
如图,是一台自动测温仪记录的图象,它反映了我市冬季某天气温T随时间t变化而变化的关系,观察图象得到下列信息,其中错误的是( )
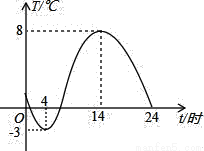
A. 凌晨4时气温最低为-3℃
B. 14时气温最高为8℃
C. 从0时至14时,气温随时间增长而上升
D. 从14时至24时,气温随时间增长而下降
C 【解析】试题分析:A.∵由图象可知,在凌晨4点函数图象在最低点﹣3,∴凌晨4时气温最低为﹣3℃,故本选项正确; B.∵由图象可知,在14点函数图象在最高点8,∴14时气温最高为8℃,故本选项正确; C.∵由图象可知,从4时至14时,气温随时间增长而上上升,不是从0点,故本选项错误; D.∵由图象可知,14时至24时,气温随时间增长而下降,故本选项正确. 故选C. ...查看答案和解析>>
科目:初中数学 来源:北师大版数学七年级下册第四章4.4用尺规作三角形课时练习 题型:填空题
已知:  ,求作
,求作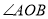 的平分线;根据第16题图所示,填写作法:
的平分线;根据第16题图所示,填写作法:
①_________________________________________________________________.
② _________________________________________________________________.
③ _________________________________________________________________.
查看答案和解析>>
科目:初中数学 来源:北师大版数学七年级下册第四章4.4用尺规作三角形课时练习 题型:单选题
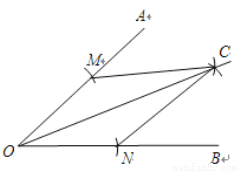
如图,直线CP是AB的中垂线且交AB于P,其中AP=2CP.甲、乙两人想在AB上取两点D、E,使得AD=DC=CE=EB,其作法如下:
甲:作∠ACP、∠BCP之角平分线,分别交AB于D、E,则D、E即为所求;
乙:作AC、BC之中垂线,分别交AB于D、E,则D、E即为所求.
对于甲、乙两人的作法,下列判断何者正确( )
A. 两人都正确 B. 两人都错误 C. 甲正确,乙错误 D. 甲错误,乙正确
D 【解析】试题解析: 甲、乙都正确, 理由是:∵CP是线段AB的垂直平分线, ∴BC=AC,∠APC=∠BPC=90°, ∵AC=2CP, ∴∠A=30°, ∴∠ACP=60°, ∵CD平分∠ACP, ∴∠ACD=∠ACP=30°, ∴∠ACD=∠A, ∴AD=DC, 同理CE=BE, 即D、E为所求; ∵D在A...查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下4.1.1 三角形及其内角和 同步练习 题型:单选题
在△ABC中,∠A=20°,∠B=60°,则△ABC的形状是( )
A. 锐角三角形 B. 钝角三角形 C. 直角三角形 D. 锐角三角形或钝角三角形
B 【解析】试题分析:由三角形内角和定理可得:∠C=180°-∠A-∠B=180°-20°-60°=100°, 所以△ABC是钝角三角形. 故选B.查看答案和解析>>
科目:初中数学 来源:2017年北师大七年级下1.5《平方差公式》练习题 题型:单选题
若M(3x-y2)=y4-9x2,那么代数式M应是( )
A. -3x-y2 B. -y2+3x C. 3x+y2 D. 3x-y2
A 【解析】M(3x-y2)=y4-9x2,变形为-M(y2-3x)=y4-9x2, 根据平方差公式(a+b)(a-b)=a2-b2,可得-M=y2+3x, 则M=-3x-y2. 故选A.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com