
已知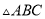 是等腰三角形,周长是
是等腰三角形,周长是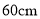 ,腰长为
,腰长为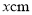 ,底为
,底为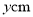 .
.
(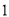 )用含
)用含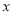 的关系式表示
的关系式表示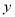 :__________.
:__________.
(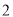 )当腰长由
)当腰长由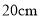 变化到
变化到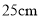 时,底边长由__________
时,底边长由__________ 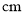 变化到__________
变化到__________ 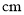 .
.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2017-2018学年八年级数学北师大版上册 全册综合测试卷 题型:单选题
直角三角形的两条直角边长分别是3,4,则该直角三角形的斜边长是( )
A. 2 B. 3 C. 4 D. 5
D 【解析】根据勾股定理即可得出答案. 【解析】 ∵直角三角形的两条直角边长分别是3,4, ∴该直角三角形的斜边长是: 故选D.查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下2.1.2 垂线的定义与性质 同步练习 题型:单选题
过一条线段外一点,作这条线段的垂线,垂足在( )
A. 这条线段上 B. 这条线段的端点处
C. 这条线段的延长线上 D. 以上都有可能
D 【解析】作一条线段的垂线,实际上是作线段所在直线的垂线,垂足可能在这条线段上,可能在端点处,也可能在线段的延长线上.查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下册4.1.2认识三角形 同步练习 题型:单选题
小李有2根木棒,长度分别为10cm和15cm,要组成一个三角形(木棒的首尾分别相连接),还需在下列4根木棒中选取( )
A. 4cm长的木棒 B. 5cm长的木棒 C. 20cm长的木棒 D. 25cm长的木棒
C 【解析】设第三根木棒的长为xcm, ∵2根木棒的长度分别为10cm和15cm, ∴15-10<x<15+10,即5<x<25, ∴四个选项中只有20cm的木棒符合条件, 故选C.查看答案和解析>>
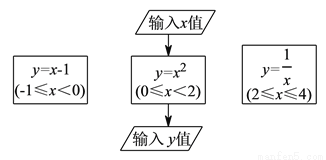
科目:初中数学 来源:北师大版七年级数学下册同步要点3.2 用关系式表示的变量间关系 题型:单选题
根据如图所示的程序,若输入的自变量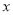 的值为
的值为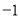 ,则输出的因变量
,则输出的因变量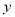 的值为 ( ).
的值为 ( ).
A. 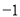 B.
B. 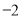 C.
C. 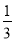 D.
D. 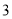
查看答案和解析>>
科目:初中数学 来源:北师大版七年级下册 第一章 整式的乘除 单元测试卷 题型:解答题
当x、y为何值时,代数式x2+y2+4x-6y+15有最小值?并求出最小值.
=-2,y=3时,代数式有最小值为2. 【解析】试题分析:本题将待求式变形为(x+2)2+(y?3)2+2,进而利用完全平方式的特征,问题即可迎刃而解. 试题解析:对代数式变形,得:(x2+4x+4)+(y2?6y+9)+2 由完全平方公式,得:(x+2)2+(y?3)2+2 观察上式发现:(x+2)2≥0,(y?3)2≥0 所以当x=-2,y=3时,待求式有最小值,...查看答案和解析>>
科目:初中数学 来源:北师大版七年级下册 第一章 整式的乘除 单元测试卷 题型:填空题
计算:20152-2×2015×2014+20142=__.
1 【解析】20152-2×2015×2014+20142=(2015-2014)2=12=1. 故答案为:1.查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下3.2 用关系式表示的变量间关系 同步练习 题型:单选题
已知三角形ABC的底边BC上的高为8 cm,当底边BC从16 cm变化到5 cm时,三角形ABC的面积( )
A. 从20 cm2变化到64 cm2 B. 从64 cm2变化到20 cm2
C. 从128 cm2变化到40 cm2 D. 从40 cm2变化到128 cm2
B 【解析】∵△ABC中,BC=16cm,BC上的高为8cm, ∴此时S△ABC=(cm3); 同理可得:当BC=5cm,BC上的高为8cm时,S△ABC=20cm3; ∴△ABC的面积从64cm3变化到20cm3. 故选B.查看答案和解析>>
科目:初中数学 来源:北师大版数学七年级下册第四章4.4用尺规作三角形课时练习 题型:解答题
尺规作图:如图,已知△ABC.
求作△A1B1C1,使A1B1=AB,∠B1=∠B,B1C1=BC.
(作图要求:不写作法,不证明,保留作图痕迹)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com