
�ⲻ��ʽ�飺  ��
��

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��������У2018����꼶��ѧ����ĩģ����ѧ�Ծ� ���ͣ���ѡ��
�ө�3����2����1��0��1��������У����ȡ��һ��������Ϊa����aʹ�ù���x�IJ���ʽ��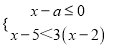 �⣬�ҹ���x�ķ�ʽ����
�⣬�ҹ���x�ķ�ʽ����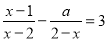 ��������ĸ���Ϊ��������
��������ĸ���Ϊ��������
A. 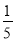 B.
B. 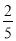 C.
C. 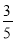 D.
D. 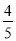
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ��̨��2017-2018ѧ����ѧ����ĩ���Ծ��꼶��ѧ�Ծ� ���ͣ������
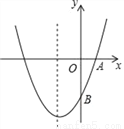
��ͼ����֪������y=ax2+bx+c��a��0���ĶԳ���Ϊֱ��x=��1���Ҿ�A��1��0����
B��0����3�����㣮��1���������ߵĽ���ʽ��
��2���������ߵĶԳ���x=��1�ϣ��Ƿ���ڵ�M��ʹ������A�ľ����뵽��B�ľ���֮����С��������������M�����꣬�����������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ��̨��2017-2018ѧ����ѧ����ĩ���Ծ��꼶��ѧ�Ծ� ���ͣ���ѡ��
��֪Բ�ĵ���뾶Ϊ6��ĸ�߳�Ϊ8��Բ�IJ����Ϊ�� ��
A. 60 B. 48 C. 60�� D. 48��
D ���������������� Բ�IJ����=•2��•6��8=48�У���ѡD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ��̨��2017-2018ѧ����ѧ����ĩ���Ծ��꼶��ѧ�Ծ� ���ͣ���ѡ��
��������y=x2����ƽ��1����λ���ȣ�������ƽ��2����λ�������õ������߽���ʽΪ��������
A. y=��x��1��2+2 B. y=��x+1��2+2 C. y=��x��1��2��2 D. y=��x+1��2��2
A ���������������� ��������y=x2����ƽ��1����λ���ȣ�������ƽ��2����λ�������õ������߽���ʽΪy=��x��1��2+2����ѡA���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2017-2018ѧ����꼶��ѧ����ĩ��ϰ�����ѧ�Ծ� ���ͣ������
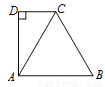
��ͼ����ABCΪ�ȱ������Σ�DC��AB��AD��CD��D������ABC���ܳ�Ϊ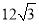 cm����
cm����
CD =________________cm��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2017-2018ѧ����꼶��ѧ����ĩ��ϰ�����ѧ�Ծ� ���ͣ���ѡ��
��P������Ϊ��2��a��3a+6�����ҵ���������ľ�����ȣ����P������Ϊ��������
A. ��3��3�� B. ��3����3�� C. ��6����6�� D. ��3��3����6����6��
D ���������������� �ߵ�P������Ϊ��2��a��3a+6�����ҵ���������ľ�����ȣ���|2��a|=|3a+6|����2��a=����3a+6�������a=��1��a=��4������P������Ϊ��3��3����6����6������ѡD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2017-2018ѧ����꼶��ѧ����ĩ��ϰ�����ѧ�Ծ� ���ͣ������
�ÿ�ѧ���������㣬����˳��  �Ľ����________ ��
�Ľ����________ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2017-2018ѧ����꼶��ѧ����ĩģ����ѧ�Ծ� ���ͣ���ѡ��
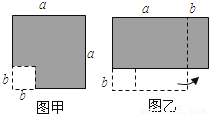
�ڱ߳�Ϊa������������ȥһ���߳�Ϊb��С�����Σ�a��b������ͼ�ף��������µIJ���ƴ��һ�����Σ���ͼ�ң�����������ͼ������Ӱ���ֵ������ȣ�������֤��ʽ�� ��
A����a+b��2=a2+2ab+b2
B����a-b��2=a2-2ab+b2
C��a2-b2=��a+b����a-b��
D����a+b����a-2b��=a2-ab-2b2
C�� �������� �����������ͼ������Ӱ���ֵ����=a2-b2��ͼ������Ӱ���ֵ����=��a+b����a-b���� ������ͼ������Ӱ���ֵ������ȣ� ����Ӱ���ֵ����=a2-b2=��a+b����a-b���� ��ѡC���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com