练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    将抛物线y=x2向右平移1个单位长度，再向上平移2个单位长度所得的抛物线解析式为（　　）

    A. y=（x﹣1）2+2 B. y=（x+1）2+2 C. y=（x﹣1）2﹣2 D. y=（x+1）2﹣2

    A 【解析】【解析】 将抛物线y=x2向右平移1个单位长度，再向上平移2个单位长度所得的抛物线解析式为y=（x﹣1）2+2．故选A．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：重庆市校2018届九年级上学期期末模拟数学试卷 题型：填空题

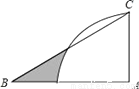
    如图，Rt△ABC中，∠A=90°，∠B=30°，AC=6，以A为圆心，AC长为半径画四分之一圆，则图中阴影部分面积为__________。（结果保留π）

    9﹣3π 【解析】试题解析：连结AD． ∵直角△ABC中，∠A=90°，∠B=30°，AC=6， ∴∠C=60°，AB=6， ∵AD=AC， ∴三角形ACD是等边三角形， ∴∠CAD=60°， ∴∠DAE=30°， ∴图中阴影部分的面积=

    查看答案和解析>>

    科目：初中数学 来源：重庆市秀山县2017-2018学年八年级上学期八校联考数学试卷 题型：单选题

    下列四组线段中，可以组成三角形的是

    A. 1，2，3 B. 2，3，4 C. 4，4，8 D. 3，4，9

    B 【解析】A、∵1+2=3，∴不能组成三角形，故A选项错误；B、∵2+3>4，∴能组成三角形，故B选项正确；C、∵4+4=8，∴不能组成三角形，故C选项错误；D、∵4+3<9，∴不能组成三角形，故D选项错误， 故选B．

    查看答案和解析>>

    科目：初中数学 来源：江苏省东台市2017-2018学年上学期期末考试九年级数学试卷 题型：填空题

    AB为半圆O的直径，现将一块等腰直角三角板如图放置，锐角顶点P在半圆上，斜边过点B，一条直角边交该半圆于点Q.若AB=2，则线段BQ的长为___________．

    【解析】如图，连接AQ，由题意可知：∠BPQ=45°， ∵AB是半圆O的直径， ∴∠AQB=90°， 又∵∠BAQ=∠BPQ=45°， ∴△ABQ是等腰直角三角形， ∴BQ=AQ=. 即，答案为.

    查看答案和解析>>

    科目：初中数学 来源：江苏省东台市2017-2018学年上学期期末考试九年级数学试卷 题型：单选题

    有15位同学参加智力竞赛,已知他们的得分互不相同,取8位同学进入决赛,小明同学知道了自己的分数后,想知道自己能否进入决赛,还需知道这15位同学的分数的( )

    A. 平均数 B. 众数 C. 中位数 D. 最高分数

    C 【解析】【解析】 由于15个人中，第8名的成绩是中位数，故小方同学知道了自己的分数后，想知道自己能否进入决赛，还需知道这十五位同学的分数的中位数．故选C．

    查看答案和解析>>

    科目：初中数学 来源：湖南省2017-2018学年八年级数学上期末复习检测数学试卷 题型：解答题

    解不等式组： ．

    ﹣2＜x≤． 【解析】首先解每个不等式，两个不等式的解集的公共部分就是不等式组的解集，然后求出x的最小正数解． 【解析】 解①得x＞﹣2， 解②得x≤， 则不等式组的解集是﹣2＜x≤． ∴x的最小整数解为-1． “点睛”本题考查了一元一次不等式组的解法：解一元一次不等式组时，一般先求出其中各不等式的解集，再求出这些解集的公共部分，解集的规律：同大取大；同小取小...

    查看答案和解析>>

    科目：初中数学 来源：湖南省2017-2018学年八年级数学上期末复习检测数学试卷 题型：填空题

    已知x是实数且满足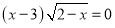，则相应的代数式x2+2x﹣1的值为________ ．

    7． 【解析】∵x是实数且满足（x﹣3）=0， ∴x﹣3=0或=0，解得x=3或x=2， ∵当x=3时，2﹣3=﹣1＜0，此时无意义， ∴x=2， 当x=2时，原式=4+4﹣1=7， 故答案为：7．

    查看答案和解析>>

    科目：初中数学 来源：湖南省2017-2018学年八年级数学上期末复习检测数学试卷 题型：解答题

    已知一个正数的平方根是a+3和2a﹣15，b的立方根是﹣2，求﹣b﹣a的平方根．

    ±2． 【解析】试题分析：根据一个数的平方根互为相反数，有a+3+2a﹣15=0，可求出a值，由b的立方根是﹣2，可求出b值，继而代入即可求出答案． 试题解析：【解析】 ∵一个数的平方根互为相反数，有a+3+2a﹣15=0，解得：a=4．又∵b的立方根是﹣2，解得：b=﹣8，∴﹣b﹣a=4，其平方根为：±2，即﹣b﹣a的平方根为±2．

    查看答案和解析>>

    科目：初中数学 来源：湖南省2017-2018学年八年级数学上期末复习检测数学试卷 题型：单选题

    如图，将一边长为a的正方形（最中间的小正方形）与四块边长为b的正方形（其中b＞a）拼接在一起，则四边形ABCD的面积为（　　）

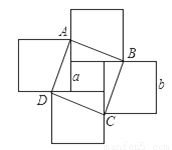
    A. b2+（b﹣a）2 B. b2+a2 C. （b+a）2 D. a2+2ab

    A 【解析】【解析】 ∵DE=b﹣a，AE=b，∴S四边形ABCD=4S△ADE+a2=4××（b﹣a）•b=b2+（b﹣a）2 ．故选A．

    查看答案和解析>>

    同步练习册答案