
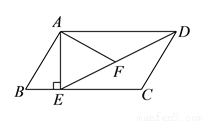
在平行四边形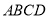 中,过点
中,过点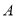 作
作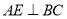 ,垂足为
,垂足为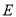 ,连接
,连接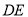 ,
, 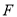 为线段
为线段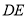 上一点,且
上一点,且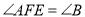 .
.
( )求证:
)求证: 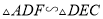 .
.
( )若
)若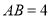 ,
, 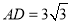 ,
, 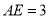 ,求
,求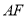 的长.
的长.
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源:江苏省泰兴市2018届九年级上学期期末考试数学试卷 题型:解答题
(1)计算: 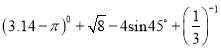 ;
;
(2)解方程: 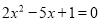 .
.
查看答案和解析>>
科目:初中数学 来源:江苏省2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
某公司有A产品40件,B产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润 (元) 如下表所示:
A产品的利润/元 | B产品的利润/元 | |
甲店 | 200 | 170 |
乙店 | 160 | 150 |
(1) 设分配给甲店A产品x件,这家公司卖出这100件产品的总利润为W (元),求W关于x的函数关系式,并求出x的取值范围;
(2) 若要求总利润不低于17560元;有多少种不同的分配方案? 并将各种方案设计出来;
(3) 为了促销,公司决定仅对甲店A产品让利销售,每件让利a元,但让利后A产品的每件利润仍高于甲店B产品的每件利润.甲店的B产品以及乙店的A,B产品的每件利润不变,问该公司又如何设计分配方案,使总利润达到最大?
(1)10≤x≤40; (2)详见解析;(3)当x=10时,利润最大. 【解析】试题分析:(1)分配给甲店A型产品x件,则分配给甲店B型产品(70-x)件,分配给乙店A型产品(40-x)件,分配给乙店B型产品(x-10)件,根据总利润等于各利润之和进行求解;根据x≥0,40-x≥0,30-(40-x)≥0可以求出取值范围;(2)、根据W≤17560得到x的取值范围,和(1)中的取值范围得到x...查看答案和解析>>
科目:初中数学 来源:江苏省2017-2018学年八年级上学期期末考试数学试卷 题型:单选题
用四舍五入法按要求对0.05049分别取近似值,其中错误的是( )
A. 0.1(精确到0.1) B. 0.05(精确到千分位)
C. 0.05(精确到百分位) D. 0.050(精确到0.00 1)
B 【解析】A选项,因为0.05049精确到0.1的结果是0.1,所以A中结果正确; B选项,因为0.05049精确到千分位的结果是0.050,所以B中结果错误; C选项,因为0.05049精确到百分位的结果是0.05,所以C中结果正确; D选项,因为0.05049精确到0.001的结果是0.050,所以D中结果正确; 故选B.查看答案和解析>>
科目:初中数学 来源:浙江省杭州市下城区安吉路良渚实验初三上期中数学试卷 题型:填空题
如图,抛物线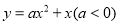 交
交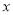 轴于点
轴于点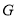 ,
, 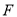 ,交
,交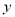 轴于点
轴于点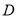 ,在
,在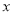 轴上方的抛物线上有两点
轴上方的抛物线上有两点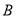 ,
, 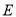 ,它们关于
,它们关于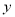 轴对称,点
轴对称,点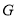 ,
, 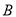 在
在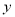 轴左侧,
轴左侧, 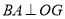 于点
于点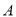 ,
, 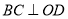 于点
于点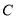 ,四边形
,四边形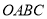 与四边形
与四边形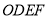 的面积分别为
的面积分别为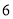 和
和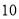 ,则
,则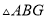 与
与 的面积之和为__________.
的面积之和为__________.
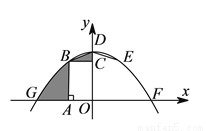
查看答案和解析>>
科目:初中数学 来源:浙江省杭州市下城区安吉路良渚实验初三上期中数学试卷 题型:单选题
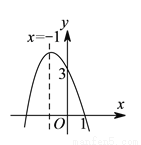
抛物线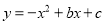 的部分图象如图所示,若
的部分图象如图所示,若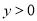 ,则
,则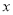 的取值范围是( ).
的取值范围是( ).
A. 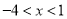 B.
B. 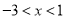 C.
C. 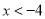 或
或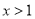 D.
D. 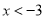 或
或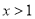
查看答案和解析>>
科目:初中数学 来源:浙江省杭州市余杭区英特外国语学校2017-2018学年八年级上学期期中数学试卷 题型:填空题
关于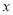 的方程
的方程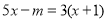 解为非负数,则
解为非负数,则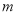 的取值范围是__________.
的取值范围是__________.
查看答案和解析>>
科目:初中数学 来源:湖北省宜昌市2018届九年级(上)期中数学试卷 题型:解答题
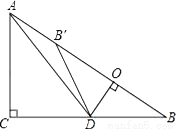
如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D为边CB上的一个动点(点D不与点B重合),过D作DO⊥AB,垂足为O,点B′在边AB上,且与点B关于直线DO对称,连接DB′,AD.
(1)求证:△DOB∽△ACB;
(2)若AD平分∠CAB,求线段BD的长;
(3)当△AB′D为等腰三角形时,求线段BD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com