练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如下图，已知经过原点的抛物线y=ax2+bx+c（a≠0）的对称轴是直线x=-1，下列结论中①ab>0，②a+b+c＞0，?③当-2＜x＜0时，y＜0．正确的个数是（　　）

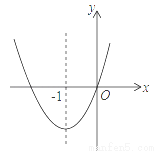
    A. 0个 B. 1个 C. 2个 D. 3个

    D 【解析】 ， . ， ， ，故①正确； ∵当 时， ， ，故②正确； ∵对称轴是直线x=﹣1，x1=0, ∴x2=-2, ∴当﹣2＜x＜0时，y＜0,故③正确； 故选Ｄ．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：江苏省扬州市2016-2017学年八年级上学期期末考试数学试卷 题型：单选题

    如图，DE是△ABC中AC边的垂直平分线，若BC=8cm，AB=10cm，则△EBC的周长为（　 ）

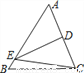
    A. 16cm B. 18cm C. 26cm D. 28cm

    B 【解析】因为：DE是△ABC中AC边的垂直平分线，所以：AD=BD, 则△DBC的周长=BD+CD+BC=AC+BC=18，故选B.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年八年级数学下册（华师大版）：期末检测1 题型：填空题

    小张参加某公司招聘测试，他的笔试、面试、计算机操作得分分别为80分，85分，90分，若三项得分依次按照25%、20%、55%确定成绩，则小王的成绩是________．

    86.5分 【解析】试题解析：2+3+5=10 根据题意得： 80×25%+85×20%+90×55% =20+17+49.5 =86.5（分） 答：小王的成绩是86.5分．

    查看答案和解析>>

    科目：初中数学 来源：广东省2018届九年级上学期学业检测（二）数学试卷 题型：解答题

    如图，已知△ABC：

    （1）求作△ABC的内切圆⊙O，与边AB、BC、AC分别相切于点D、E、F；

    （2）若AB=6，BC=8，AC=12，求AD、BE、CF的长度.

    （1）见解析；（2）AD=5，BE=1，CF=7. 【解析】试题分析：（1）分别作∠BAC、∠ABC的角平分线交于点O，过点O作OD⊥AB，垂足为D，以O为圆心，以OD长为半径画圆即可得； （2）设AD=x，由切线长定理可得AF=AD=x，BD=BE=6-x，CE=CF=12-x，列方程求解即可得. 试题解析： (1)如图所示； (2)设AD=x， 则AF=AD=x，...

    查看答案和解析>>

    科目：初中数学 来源：广东省2018届九年级上学期学业检测（二）数学试卷 题型：填空题

    在一个不透明的布袋中装有2个白球和a个黄球，它们除颜色不同外，其余均相同，若从中随机摸出一个球，摸到黄球的概率是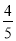，则a=______.

    8 【解析】由题意得： ，解得：a=8，经检验a=8是分式方程的解， 故答案为：8.

    查看答案和解析>>

    科目：初中数学 来源：广东省2018届九年级上学期学业检测（二）数学试卷 题型：单选题

    下列事件中是必然事件的是

    A、实心铁球投入水中会沉入水底

    B、抛出一枚硬币，落地后正面向上

    C、明天太阳从西边升起

    D、NBA篮球队员在罚球线投篮2次，至少投中一次

    A 【解析】 试题分析：A、实心铁球投入水中会沉入水底是必然事件，故正确；B、抛出一枚硬币，落地后正面向上是随机事件，故错误；C、明天太阳从西边升起是不可能事件，故错误；D、NBA篮球队员在罚球线投篮2次，至少投中一次是随机事件，故错误．故选A．

    查看答案和解析>>

    科目：初中数学 来源：湖北省孝感市八校联谊2017-2018学年九年级上册数学12月联考试卷 题型：解答题

    已知关于x的一元二次方程 x2-6x+m+4=0有两个实数根 x1，x2.

    （1）求m的取值范围；

    （2）若 x1，x2满足x2-2x1=-3 ，求m的值.

    （1）m≤5;（2）m=5. 【解析】试题分析： （1）由原方程有两个实数根可知：根的判别式△，由此列出关于“m”的表达式，解不等式即可求得m的取值范围； （2）由方程 x2-6x+m+4=0有两个实数根 x1，x2可得：x1+x2=6，x1·x2=m+4，结合x2-2x1=-3即可解得m的值. 试题解析： （1）∵关于x的一元二次方程x2-6x+m+4 有实数根， ...

    查看答案和解析>>

    科目：初中数学 来源：湖北省孝感市八校联谊2017-2018学年九年级上册数学12月联考试卷 题型：单选题

    抛物线y=2x2-12x+22 的顶点是（    ）

    A. (3,-4) B. (-3，4) C. (3，4) D. (2，4)

    C 【解析】∵， ∴抛物线的顶点坐标为（3，4）. 故选C.

    查看答案和解析>>

    科目：初中数学 来源：北京市海淀区2017-2018学年八年级上学期期末考试数学试卷 题型：填空题

    如图，在平面直角坐标系xOy中，△DEF可以看作是△ABC经过若干次的图形变化（轴对称、平移）得到的，写出一种由△ABC得到△DEF的过程：____________．

    答案不唯一，如：将△ABC关于y轴对称，再将三角形向上平移3个单位长度 【解析】将△ABC关于y轴对称，再将三角形向上平移3个单位长度得到△DEF； 或：将△ABC向上平移3个单位长度，再关于y轴对称得到△DEF， 故答案为：答案不唯一，如：将△ABC关于y轴对称，再将三角形向上平移3个单位长度得到△DEF.

    查看答案和解析>>

    同步练习册答案