练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    在一个不透明的口袋中装有12个白球、16个黄球、24个红球、28个绿球，除颜色其余都相同，小明通过多次摸球实验后发现，摸到某种颜色的球的频率稳定在0.3左右，则小明做实验时所摸到的球的颜色是（　　）

    A. 白色 B. 黄色 C. 红色 D. 绿色

    C 【解析】试题解析：因为白球的概率为： ； 因为黄球的概率为： ＝0.2； 因为红球的概率为： ＝0.3； 因为绿球的概率为： ＝0.35． 故选C．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：北师大版数学七年级下册第一章整式乘法1.2幂的乘方与积的乘方课时练习 题型：单选题

    下面计算正确的是（ ）。

    A. a5 + a5= 2a10 B. （ x3）3 = x10 C. （－32）4=38 D. x3 + y3 =（x+y）3

    C 【解析】试题解析：：A项计算得2a5 ， B项计算得 x9 ， D项不能计算 ，故C项正确. 故选C.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年八年级数学北师大版上册 第1-4章综合测试卷 题型：填空题

    若第四象限内的点P(x，y)满足|x|＝2，y2＝36，则点P的坐标是________．

    (2，－6) 【解析】试题解析： ∵点在第四象限内， ∴点P的坐标为 故答案为：

    查看答案和解析>>

    科目：初中数学 来源：北师大版九年级下册数学全册综合测试卷二 题型：解答题

    （6分）如图①所示，将直尺摆放在三角板ABC上，使直尺与三角板的边分别交于点D，E，F，G，量得∠CGD=42°。

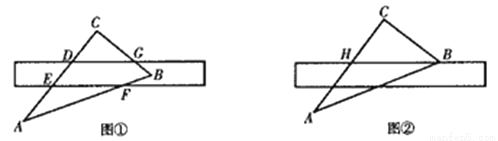
    （1）求∠CEF的度数；

    （2）将直尺向下平移，使直尺的边缘通过三角板的顶点B，交AC边于点H，如图②所示．点H，B在直尺上的读数分别为4，13．4，求BC的长（结果保留两位小数）．

    （参考数据：sin42°≈0．67，cos42°≈0．74，tan42°≈0．90）

    （1）∠CEF=48°； （2）BC的长为6．96m． 【解析】试题分析：（1）由DG//EF，可知要求∠CEF的度数，需求出∠CDG的度数，而在△CDG在，∠C=90°，∠CGD＝42°，从而得解． （2）由已知可得∠ＣＢＨ＝42°，由三角函数即可得； 试题解析：（1）∵ ∠CGD＝42°，∠C＝90°，∴ ∠CDG＝90°－ 42°＝48°，∵ DG∥EF， ∴∠CEF...

    查看答案和解析>>

    科目：初中数学 来源：北师大版九年级下册数学全册综合测试卷二 题型：填空题

    弦AB将⊙O分成度数之比为1：5的两段弧，则∠AOB=________°．

    60 【解析】试题解析：∵弦AB将圆分成的两段弧所对的圆心角度数之比为1：5， ∴∠AOB=×360°=60°， 故答案为：60．

    查看答案和解析>>

    科目：初中数学 来源：北师大版九年级下册数学全册综合测试卷二 题型：单选题

    如图，已知灯塔M方圆一定范围内有镭射辅助信号，一艘轮船在海上从南向北方向以一定的速度匀速航行，轮船在A处测得灯塔M在北偏东30°方向，行驶1小时后到达B处，此时刚好进入灯塔M的镭射信号区，测得灯塔M在北偏东45°方向，则轮船通过灯塔M的镭射信号区的时间为（　　）

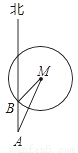
    A. 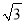（﹣1）小时 B. 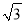（+1）小时 C. 2小时 D. 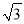小时

    B 【解析】试题解析：连接MC，过M点作MD⊥AC于D． 在Rt△ADM中，∵∠MAD=30°， ∴AD=MD， 在Rt△BDM中，∵∠MBD=45°， ∴BD=MD， ∴BC=2MD， ∴BC：AB=2MD：（-1）MD=2： +1． 故轮船通过灯塔M的镭射信号区的时间为（+1）小时． 故选B．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年度人教版九年级数学下册第26 章同步课时练习：26.1.1 反比例函数 题型：解答题

    一辆汽车往返于甲、乙两地之间，如果汽车以50千米/时的平均速度从甲地出发，则6小时可到达乙地．

    （1）写出时间t（时）关于速度v（千米/时）的函数关系式，并画出函数图象．

    （2）若这辆汽车需在5小时内从甲地到乙地，则此时汽车的平均速度至少应是多少？

    （1）t=．（2）汽车的平均速度至少为60千米/时． 【解析】试题分析：（1）利用时间t与速度v成反比例可以得到反比例函数的解析式； （2）令t=5，求得v值即可． 试题解析：（1）设函数关系式为． ∵汽车以50千米/时的平均速度从甲地出发，则6小时可到达乙地． ∴6=． 解得k=300． ∴时间t（时）关于速度v（千米/时）的函数关系式为t=． （2）...

    查看答案和解析>>

    科目：初中数学 来源：北师大版九年级下册数学全册综合测试卷一 题型：解答题

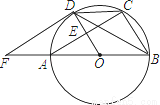
    如图，AB是⊙O的直径，AC是弦，半径OD⊥AC于点E，过点D的切线与BA延长线交于点F．

    （1）求证：∠CDB=∠BFD；

    （2）若AB=10，AC=8，求DF的长．

    （1）证明见解析（2） 【解析】试题分析：（1）根据切线的性质得到DF⊥OD，由于OD⊥AC，推出DF∥AC，根据平行线的性质得到∠CAB=∠BFD，于是得到结论； （2）利用垂径定理得出AE的长，再利用相似三角形的判定与性质得出FD的长． 试题解析：（1）∵DF与⊙O相切， ∴DF⊥OD， ∵OD⊥AC， ∴DF∥AC， ∴∠CAB=∠BFD， ∴...

    查看答案和解析>>

    科目：初中数学 来源：人教版八年级下册数学全册综合测试二 题型：单选题

    “爱心小组”的九位同学为灾区捐款，捐款金额分别为20，10，15，15，18，17，12，14，11（单位：元）．那么这组数据的中位数是（　　）

    A. 18 B. 15 C. 14 D. 17

    B 【解析】试题解析：将这组数据从小到大的顺序排列后，处于中间位置的那个数是15，那么由中位数的定义可知，这组数据的中位数是15． 故选B．

    查看答案和解析>>

    同步练习册答案