
一辆汽车往返于甲、乙两地之间,如果汽车以50千米/时的平均速度从甲地出发,则6小时可到达乙地.
(1)写出时间t(时)关于速度v(千米/时)的函数关系式,并画出函数图象.
(2)若这辆汽车需在5小时内从甲地到乙地,则此时汽车的平均速度至少应是多少?
(1)t=.(2)汽车的平均速度至少为60千米/时. 【解析】试题分析:(1)利用时间t与速度v成反比例可以得到反比例函数的解析式; (2)令t=5,求得v值即可. 试题解析:(1)设函数关系式为. ∵汽车以50千米/时的平均速度从甲地出发,则6小时可到达乙地. ∴6=. 解得k=300. ∴时间t(时)关于速度v(千米/时)的函数关系式为t=. (2)...科目:初中数学 来源:2017-2018学年九年级数学北师大版上册 第2章 一元二次方程 单元测试卷 题型:解答题
“a2=0”这个结论在数学中非常有用,有时我们需要将代数式配成完全平方式,例如:x2+4x+5=x2+4x+4+1=(x+2)2+1,∵(x+2)2≥0,(x+2)2+1≥1,∴x2+4x+5≥1.试利用“配方法”解决下列问题:
(1)填空:因为x2﹣4x+6=(x )2+ ;所以当x= 时,代数式x2﹣4x+6有最 (填“大”或“小”)值,这个最值为 .
(2)比较代数式x2﹣1与2x﹣3的大小.
(1)﹣2;2;2;小;2;(2)x2﹣1>2x﹣3. 【解析】试题分析:(1)把原式利用平方法化为完全平方算与一个常数的和的形式,利用偶次方的非负性解答; (2)利用求差法和配方法解答即可. 试题解析:(1)x2-4x+6=(x-2)2+2, 所以当x=2时,代数式x2-4x+6有最小值,这个最值为2, 故答案为:-2;2;2;小;2; (2)x2-1-(2x...查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学北师大版上册 第1-4章综合测试卷 题型:单选题
如图,Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为( )
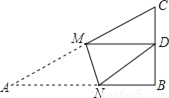
A.  B.
B.  C. 4 D. 5
C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源:北师大版九年级下册数学全册综合测试卷二 题型:单选题
在一个不透明的口袋中装有12个白球、16个黄球、24个红球、28个绿球,除颜色其余都相同,小明通过多次摸球实验后发现,摸到某种颜色的球的频率稳定在0.3左右,则小明做实验时所摸到的球的颜色是( )
A. 白色 B. 黄色 C. 红色 D. 绿色
C 【解析】试题解析:因为白球的概率为: ; 因为黄球的概率为: =0.2; 因为红球的概率为: =0.3; 因为绿球的概率为: =0.35. 故选C.查看答案和解析>>
科目:初中数学 来源:北师大版九年级下册数学全册综合测试卷二 题型:单选题
已知两圆相交,它们的圆心距为3,一个圆的半径是2,那么另一个圆的半径长可以是( )
A. 1 B. 3 C. 5 D. 7
B 【解析】两圆相交时,两半径之差<圆心距<两半径之和,故选B.查看答案和解析>>
科目:初中数学 来源:2017-2018学年度人教版九年级数学下册第26 章同步课时练习:26.1.1 反比例函数 题型:填空题
反比例函数y=-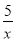 ,当x=-3时,y=___________.
,当x=-3时,y=___________.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年度人教版九年级数学下册第26 章同步课时练习:26.1.1 反比例函数 题型:单选题
若反比例函数y=- 的图象一定经过点( )
的图象一定经过点( )
A. (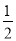 ,-2) B. (1,2 C. (-1,
,-2) B. (1,2 C. (-1, 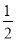 ) D. (1,-2)
) D. (1,-2)
查看答案和解析>>
科目:初中数学 来源:北师大版九年级下册数学全册综合测试卷一 题型:单选题
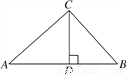
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D.若AC=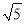 ,BC=2,则sin∠ACD的值为( )
,BC=2,则sin∠ACD的值为( )
A. 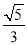 B.
B. 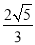 C.
C. 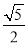 D.
D. 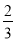
查看答案和解析>>
科目:初中数学 来源:人教版七年级下册数学第7-10章综合测试卷 题型:解答题
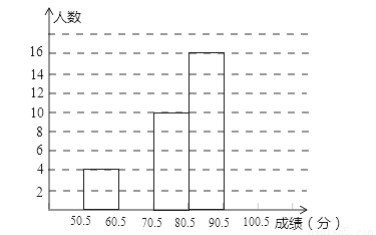
为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有850名学生参加了这次竞赛,为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取整数,满分为100分)进行统计.请你根据尚未完成并有局部污染的频率分布表和频率分布直方图,解答下列问题:
分 组 | 频数 | 频率 |
50.5~60.5 | 4 | 0.08 |
60.5~70.5 | 0.16 | |
70.5~80.5 | 10 | |
80.5~90.5 | 16 | 0.32 |
90.5~100.5 | ||
合 计 | 50 | 1.00 |
(1)填充频率分布表的空格;
(2)补全频数直方图,并在此图上直接绘制频数分布折线图;
(3)全体参赛学生中,竞赛成绩落在哪组范围内的人数最多?
(4)若成绩在90分以上(不含90分)为优秀,则该校成绩优秀的约为多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com