练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    列出下列问题中的函数关系式，并判断它们是否为反比例函数．

    （1）某农场的粮食总产量为1 500t，则该农场人数y（人）与平均每人占有粮食量x（t）的函数关系式；

    （2）在加油站，加油机显示器上显示的某一种油的单价为每升4.75元，总价从0元开始随着加油量的变化而变化，则总价y（元）与加油量x（L）的函数关系式；

    （3）小明完成100m赛跑时，时间t（s）与他跑步的平均速度v（m/s）之间的函数关系式．

    （1）y=是反比例函数；（2）y=4.75x是正比例函数；（3）t=是反比例函数 【解析】试题分析: （1）由平均数,得x=，即y=是反比例函数, （2）由单价乘以油量等于总价,得y=4.75x,即y=4.75x是正比例函数, （3）由路程与时间的关系,得t=,即t=是反比例函数． 试题解析:（1）由平均数,得x=，即y=是反比例函数, （2）由单价乘以油量等于总价,...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：人教版 2018年春 七年级数学下册 第五章 相交线与平行线 几何证明题 题型：解答题

    如图，已知AC∥DE，DC∥EF，CD平分∠BCD．求证：EF平分∠BED．

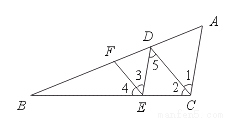
    证明见解析 【解析】试题分析：先根据平行线的性质得出∠1=∠5，∠5=∠3，得到∠1=∠3，再由平行线的性质得到∠2=∠4，再根据CD平分∠ACB可知∠1=∠2，故可得出结论． 试题解析：证明：∵AC∥DE（已知），∴∠1=∠5． 同理∠5=∠3，∴∠1=∠3． ∵DC∥EF（已知），∴∠2=∠4． ∵CD平分∠ACB，∴∠1=∠2，∴∠3=∠4，∴EF平分∠BED．...

    查看答案和解析>>

    科目：初中数学 来源：北师大版八年级下册数学全册综合测试卷 题型：填空题

    已知点P（﹣b，2）与点Q（3，2a）关于原点对称，则a= ，b= ．

    ﹣1，3． 【解析】 试题分析：根据两个点关于原点对称时，它们的坐标符号相反，即点P（x，y）关于原点O的对称点是P′（﹣x，﹣y），∵点P（﹣b，2）与点Q（3，2a）关于原点对称， ∴﹣b=﹣3，﹣2=2a，∴b=3，a=﹣1． 故答案为：﹣1，3．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年度人教版九年级数学下册第26 章同步课时练习：26.2 实际问题与反比例函数（第2课时） 题型：解答题

    你吃过拉面吗？实际上在做拉面的过程中就渗透着数学知识：一定体积的面团做成拉面时，面条的总长度y（m）是面条的粗细（横截面积）S（mm2）的反比例函数，其图象如图所示．

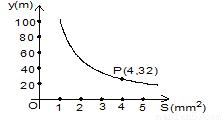
    （1）写出y（m）与S（mm2）的函数关系式；

    （2）求当面条横截面积为1．6 mm2时，面条的总长度是多少米？

    （1）；（2）80m． 【解析】 试题分析：（1）本题考查反比例函数的图象和性质，由图象可以看出点P（4，32）在反比例函数图象上，由此可得反比例函数的解析式； （2）当时，代入函数解析式即可得出 试题解析：（1）设函数关系式为：，把P（4，32）代入得：k=128，∴； （2）当时，

    查看答案和解析>>

    科目：初中数学 来源：广东省2017-2018学年度九年级（上）数学第一次月考试卷（11月份）(解析版) 题型：解答题

    已知反比例函数y=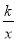的图象与一次函数y=kx+m的图象相交于点A（2，1）．

    （1）分别求出这两个函数的解析式；

    （2）当x取什么范围时，反比例函数值大于0；

    （3）若一次函数与反比例函数另一交点为B，且纵坐标为﹣4，当x取什么范围时，反比例函数值大于一次函数的值；

    （4）试判断点P（﹣1，5）关于x轴的对称点P′是否在一次函数y=kx+m的图象上．

    （1）y=，y=2x﹣3；（2）x＞0；（3）x＜﹣0.5或0＜x＜2；（4）点P′在直线上． 【解析】试题分析：（1）根据题意，反比例函数y=的图象过点A（2，1），可求得k的值，进而可得解析式；一次函数y=kx+m的图象过点A（2，1），代入求得m的值，从而得出一次函数的解析式；（2）根据（1）中求得的解析式，当y＞0时，解得对应x的取值即可； （3）由题意可知，反比例函数值大于一...

    查看答案和解析>>

    科目：初中数学 来源：广东省2017-2018学年度九年级（上）数学第一次月考试卷（11月份）(解析版) 题型：填空题

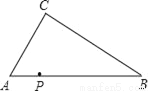
    如图，点P是Rt△ABC斜边AB上的任意一点（A、B两点除外），过点P作一条直线，使截得的三角形与Rt△ABC相似，这样的直线可以作_____条．

    3 【解析】 过点P分别作三边的垂线,所得△ADP, △AEP, △BPF与RtΔABC相似. 所以这样的直线能做三条.

    查看答案和解析>>

    科目：初中数学 来源：广东省2017-2018学年度九年级（上）数学第一次月考试卷（11月份）(解析版) 题型：填空题

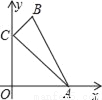
    如图，在平面直角坐标系中，点A是x轴正半轴上的一个动点，点C是y轴正半轴上的点，BC⊥AC于点C．已知AC=8，BC=3．

    （1）线段AC的中点到原点的距离是_____；

    （2）点B到原点的最大距离是_____．

    4 9 【解析】(1)因为∠AOC=90°,AC=8,所以线段AC的中点到原点的距离是: ,AC=4, (2)取AC的中点E,连接BE,OE,OB, 因为∠AOC=90°,AC=8,所以OE=CE=,AC=4, 因为BC⊥AC,BC=3, 所以BE=5, 若点O,E,B不在一条直线上,则OB

    查看答案和解析>>

    科目：初中数学 来源：2018届九年级中考数学专题复习同步练习题：平行四边形 题型：填空题

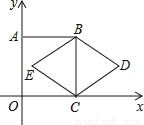
    如图，正方形ABCO的顶点C、A分别在x轴、y轴上，BC是菱形BDCE的对角线，若∠D=60°，BC=2，则点D的坐标是_____．

    （2+，1）． 【解析】试题解析：过点D作DG⊥BC于点G， ∵四边形BDCE是菱形， ∴BD=CD． ∵BC=2，∠D=60°， ∴△BCD是等边三角形， ∴BD=BC=CD=2， ∴CG=1，GD=CD•sin60°=2×=， ∴D（2+，1）．

    查看答案和解析>>

    科目：初中数学 来源：江苏省无锡市2018届九年级上学期期末考试数学试卷 题型：单选题

    -3的绝对值是（ ）

    A. 3 B. -3 C. D. -

    A 【解析】试题解析：|-3|=-（-3）=3． 故选A．

    查看答案和解析>>

    同步练习册答案