练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    在二次函数y=x2+bx+c中，函数y与自变量x之间的部分对应值如下表所示：

    x

    …

    0

    1

    2

    3

    4

    5

    …

    y

    …

    8

    3

    0

    ﹣1

    0

    3

    …

    若点A（﹣1，m），B（6，n），则m_____n．（选填“＞”、“＜”或“=”）

    ＞ 【解析】由表格中数据可得，抛物线的对称轴为：直线x=3， 由a=1，可得抛物线开口向上， ∵3?(?1)=4，6?3=3， ∴B点距离对称轴距离近， ∴m>n. 故答案为：>.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017年天津二十一中中考数学冲刺试卷（2） 题型：单选题

    如图,二次函数y=ax2+bx+c（a≠0）的图象经过点（1,2）且与x轴交点的横坐标分别为x1，x2，其中﹣1＜x1＜0.1＜x2＜2.下列结论：4a+2b+c＜0；2a+b＜0；b2+8a＞4ac；

    a＜﹣1；其中结论正确的有（ ）

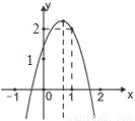
    A. 1个 B. 2个 C. 3个 D. 4个

    D 【解析】由抛物线的开口向下知a<0， 与y轴的交点为在y轴的正半轴上，得c>0， 对称轴为x= <1，∵a<0，∴2a+b<0， 而抛物线与x轴有两个交点,∴ ?4ac>0， 当x=2时，y=4a+2b+c<0，当x=1时，a+b+c=2. ∵ >2，∴4ac?<8a，∴+8a>4ac， ∵①a+b+c=2，则2a+2b+2c=4，②4a+2b+c<0...

    查看答案和解析>>

    科目：初中数学 来源：2017年贵州省中考数学二模试卷 题型：解答题

    （1）计算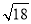： ﹣|﹣4|﹣2cos45°﹣（3﹣π）0．

    （2）先化简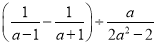然后从1、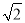 、﹣1中选取一个你认为合适的数作为a的值代入求值．

    （1） ;(2) , 【解析】试题分析：（1）根据二次根式、绝对值、锐角三角函数的性质，零次幂的性质，直接计算可求结果. （2）根据分式的混合运算和运算顺序，先把分子分母因式分解，把除化为乘，通分约分即可. 试题解析：（1）﹣|﹣4|﹣2cos45°﹣（3﹣π）0 =3﹣4﹣2×﹣1 =2﹣5； （2）（﹣） =[﹣]× =× =， 由题...

    查看答案和解析>>

    科目：初中数学 来源：2017年贵州省中考数学二模试卷 题型：单选题

    如图，直线a，b与直线c，d相交，若∠1=∠2，∠3=70°，则∠4的度数是

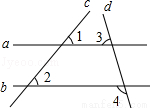
    A．35° B．70° C．90° D．110°

    D

    查看答案和解析>>

    科目：初中数学 来源：2017年吉林省长春市中考数学模拟试卷（7） 题型：解答题

    如图，某数学兴趣小组在活动课上测量学校旗杆高度，已知小明的眼睛与地面的距离AB是1.7m，看旗杆顶部M的仰角为45°，小红的眼睛与地面的距离CD是1.5m，看旗杆顶部M的仰角为30°．两人相距23m且位于旗杆两侧（点B，N，D在同一条直线上）．请求出旗杆MN的高度．【参考数据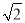：≈1.4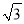， ≈1.7，结果保留整数】

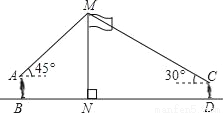
    旗杆MN的高度约为10米 【解析】首先分析图形：根据题意构造直角三角形；本题涉及到两个直角三角形，应利用其公共边构造三角关系，进而可求出答案．

    查看答案和解析>>

    科目：初中数学 来源：2017年吉林省长春市中考数学模拟试卷（7） 题型：填空题

    计算：（3a）2=_____．

    9a2 【解析】（3a）2=32×a2=9a2， 故答案为：9a2

    查看答案和解析>>

    科目：初中数学 来源：2017年吉林省长春市中考数学模拟试卷（7） 题型：单选题

    据统计，第22届冬季奥林匹克运动会的电视转播时间长达88000小时，社交网站和国际奥委会官方网站也创下冬奥会收看率纪录．用科学记数法表示88000为（　　）

    A. 0.88×105 B. 8.8×104 C. 8.8×105 D. 8.8×106

    B 【解析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数,故88000=8.8×104. 故选：B.

    查看答案和解析>>

    科目：初中数学 来源：山东省2018届九年级12月月考数学试卷 题型：单选题

    圆心角为60°，且半径为3的扇形的弧长为

    A. 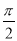B. π C. 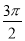D. 3π

    B 【解析】直接根据弧长公式： 进行计算即可． 【解析】 ∵圆心角为60°，且半径为3， ∴弧长= . 故选B.

    查看答案和解析>>

    科目：初中数学 来源：江苏省扬州市2016届九年级下学期二模数学试卷 题型：填空题

    已知：在等边△ABC中， AB=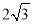， D，E分别是AB，BC的中点（如图）．若将△BDE绕点B逆时针旋转，得到△BD1E1，设旋转角为α（0°＜α＜180°），记射线CE1与AD1的交点为P．点P到BC所在直线的距离的最大值为_____________．

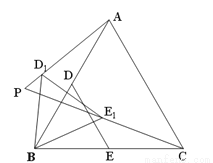
    2 【解析】∵等边△ABC，∴∠ABC=60°，AB=CB， ∵等边△D1E1B，∴∠D1BE1=60°，D1B= BE1， ∴∠D1BA=∠E1BC， 在△D1BA和△E1BC中， ， ∴△D1BA≌△E1BC（SAS）， ∴∠PAB=∠PCB， ∵∠APC+∠PAB=∠ABC+∠PCB， ∴∠APC=∠ABC=60°， ∵∠D1BE1...

    查看答案和解析>>

    同步练习册答案