
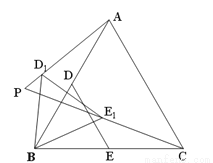
已知:在等边△ABC中, AB=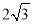 , D,E分别是AB,BC的中点(如图).若将△BDE绕点B逆时针旋转,得到△BD1E1,设旋转角为α(0°<α<180°),记射线CE1与AD1的交点为P.点P到BC所在直线的距离的最大值为_____________.
, D,E分别是AB,BC的中点(如图).若将△BDE绕点B逆时针旋转,得到△BD1E1,设旋转角为α(0°<α<180°),记射线CE1与AD1的交点为P.点P到BC所在直线的距离的最大值为_____________.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2017年吉林省长春市中考数学模拟试卷(7) 题型:填空题
在二次函数y=x2+bx+c中,函数y与自变量x之间的部分对应值如下表所示:
x | … | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 8 | 3 | 0 | ﹣1 | 0 | 3 | … |
若点A(﹣1,m),B(6,n),则m_____n.(选填“>”、“<”或“=”)
> 【解析】由表格中数据可得,抛物线的对称轴为:直线x=3, 由a=1,可得抛物线开口向上, ∵3?(?1)=4,6?3=3, ∴B点距离对称轴距离近, ∴m>n. 故答案为:>.查看答案和解析>>
科目:初中数学 来源:湖北省武汉市汉阳区2018届九年级(上)期中数学试卷(解析版) 题型:解答题
某商场销售一种产品,每件产品的成本为2400元,销售单价定位3000元,该商场为了促销,规定客户一次购买这种新型产品不超过10件时,每件按3000元销售;若一次购买该种产品超过10件时,每多购买一件,所购买的全部产品的销售单价均降低10元,但销售单价均不低于2600元;
(1)设一次购买这种产品x(x≥10)件,商场所获的利润为y元,求y(元)与x(件)之间的函数关系式,并写出自变量x的取值范围;
(2)在客户购买产品的件数尽可能少的前提下,商场所获的利润为12000元,此时该商场销售了多少件产品?
(3)填空:该商场的销售人员发现,当客户一次购买产品的件数在某一个区间时,会出现随着一次购买的数量的增多,商场所获的利润反而减少这一情况,客户一次购买产品的数量x满足的条件是 (其它销售条件不变)
(1);(2)30;(3)35<x≤50. 【解析】试题分析:(1)利用单价利润件数=利润列函数关系式,按照不同条件要列分段函数,注意求定义域.(2)令函数值为12000,解方程.(3)求二次函数的增减性, y随x的增大而减小. 试题解析: 【解析】 (1)当一次购买这种产品x(x≥10)件时,销售单价为3000﹣10(x﹣10),由题意可知,3000﹣10(x﹣10)≥260...查看答案和解析>>
科目:初中数学 来源:湖北省武汉市汉阳区2018届九年级(上)期中数学试卷(解析版) 题型:单选题
下面四个手机应用软件图标中是轴对称图形的是 ( ).
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市2016届九年级下学期二模数学试卷 题型:解答题
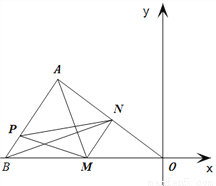
如图,在平面直角坐标系中,△AOB的三个顶点的坐标分别是A(-4,3),B(-6,0), O是原点.点M是OB边上异于O,B的一动点,过点M作MN//AB,点P是AB边上的任意点,连接AM,PM,PN,BN.设点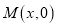 .
.
(1)求出OA所在直线的解析式,并求出点M的坐标为(-1,0)时,点N的坐标.
(2)若 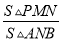 =
=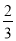 时,求此时点N的坐标.
时,求此时点N的坐标.
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市2016届九年级下学期二模数学试卷 题型:填空题
甲、乙两台机床同时生产一种零件,在5天中,两台机床每天生产出的次品数分别如下表所列.
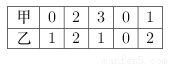
分析上述数据,请你估计这两台机床的性能_______比较稳定(填“甲”或“乙”或“无法确定”) .
乙 【解析】甲=(0+2+3+0+1)÷5=1.2, 乙=(1+2+1+0+2)÷5=1.2, S2甲= [(0-1.2)2+(2-1.2)2+(3-1.2)2+(0-1.2)2+(1-1.2)2]=1.36, S2乙= [(1-1.2)2+(2-1.2)2+(1-1.2)2+(0-1.2)2+(2-1.2)2]=0.56, S2甲>S2乙. 所以乙的性能比较稳...查看答案和解析>>
科目:初中数学 来源:江苏省扬州市2016届九年级下学期二模数学试卷 题型:单选题
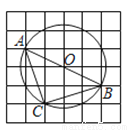
如图,在6×6的方格纸中,每个小方格都是边长为1的正方形,其中A、B、C为格点.作△ABC的外接圆⊙O,则弧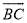 的长为( )
的长为( )
A. 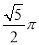 B.
B. 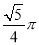 C.
C. 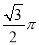 D.
D. 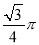
查看答案和解析>>
科目:初中数学 来源:2017年海南省海口市中考数学模拟试卷 题型:单选题
将一张宽为6的长方形纸片(足够长)折叠成如图所示图形.重叠部分是一个△ABC,则三角形ABC面积的最小值是( )
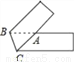
A. 9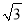 B. 18 C. 18
B. 18 C. 18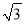 D. 36
D. 36
查看答案和解析>>
科目:初中数学 来源:2017年海南省中考数学模拟试卷 题型:解答题
兄弟二人今年分别为15岁和9岁,多少年后兄的年龄是弟的年龄的2倍?
3年前兄的年龄是弟的年龄的2倍. 【解析】试题分析:等量关系为:若干年后兄的年龄=2若干年后弟的年龄,把相关数值代入求解即可. 试题解析:设x年后,兄的年龄是弟的年龄的2倍, 则x年后兄的年龄是15+x,弟的年龄是9+x. 由题意,得2×(9+x)=15+x, 18+2x=15+x,2x﹣x=15﹣18, ∴x=﹣3. 答:3年前兄的年龄是弟的年龄的2倍....查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com