
��ͼ������ֱ�ǡ�ABC�У�AB=AC=8����ABΪֱ���İ�ԲO��б��BC��D������Ӱ�������Ϊ����������У��� ��
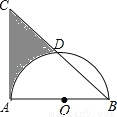
A. 16 B. 24-4�� C. 32-4�� D. 32-8��
B ���������������������AD����Ϊ��ABC�ǵ���ֱ�������Σ��ʡ�ABD=45�㣬����AB��Բ��ֱ���ó���ADB=90�㣬�ʡ�ABDҲ�ǵ���ֱ�������Σ����ԣ�S��Ӱ=S��ABC-S��ABD-S����AD�ɴ˿ɵó����ۣ� �������� ����AD��OD�� �ߵ���ֱ�ǡ�ABC�У� ���ABD=45��. ��AB��Բ��ֱ���� ���ADB=90�㣬 ���ABDҲ�ǵ���ֱ��...
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ����ѧ�˽̰���꼶�ϲ��11�µڶ������������йصĽǵ�һ��ʱͬ����ϰ ���ͣ���ѡ��
һ�������ε������ڽǺ�С�ڵ������ڽǣ�����������ǣ������������Σ�
A. ��� B. �۽� C. ֱ�� D. ����
B ���������������� �����ε������ڽǺ͵���180�ȣ�������������ڽ�֮��С�ڵ������ڽǣ�˵���������ڽǴ���90�ȣ��������������Ƕ۽������Σ���ѡB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰���꼶�ϲ� 22.3 ���κ�����Ӧ�� ͬ������ ���ͣ������
�ൺ��ij��Ƶ������ʵ�е������������ּ۸��������ÿ��ȵ������� ���±���ȥ��þƵ������ij�������ؼ�¼��
���±���ȥ��þƵ������ij�������ؼ�¼��
���� | ���� | |
δ��ס������ | 10 | 0 |
�������루Ԫ�� | 24 000 | 40 000 |
��1���þƵ�������ж��ټ䣿����ÿ��۸�Ϊ����Ԫ
��2�������������٣�������ļ������䡣���г����鷢�֣�����������Ծ�ʵ��ȥ�������۸���ôÿ�춼����������۸�������ǣ���ôÿ����25Ԫ��ÿ��δ��ס����������1�䡣�������������أ��þƵ꽫������ļ۸����Ƕ���Ԫʱ�������������������ߣ�������������Ƕ���Ԫ��
��1���þƵ��������50�䣬����ÿ��۸�Ϊ800Ԫ��2����ʱ�� �������� �����������1��������ÿ��ȵ������ǣ�������ÿ���ǵ���1�����ݴ˵�����ϵ�з�ʽ���̽�Ӧ���� ��2��������mԪ������Ϊ���۸�ÿ����25Ԫ��ÿ����ס����������1�䣬����ס������ �����������ʽ=��������ֵ. ��������� ��1�����м�����䣬����ɵ� ��ã���������ԭ���̵ĸ� �� �𣺸�...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ�ij���2018����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ������
��ͼ��С�����������ֳ�����ʱ����Ҫ������ѧ����ѧ֪ʶ����ij�����ֳ�������ɽ��AE�ij��ȣ�������ɽ���µ�E�����ɽ��A��������30�㣬Ȼ���������¶���i=1��1����tan��CED=1����б�²���15���ӵִ�C������ʱ�����A��ĸ�����15�㣮��֪С���IJ����ٶ���18��/�֣�ͼ�е�A��B��E��D��C��ͬһƽ���ڣ��ҵ�D��E��B��ͬһˮƽֱ���ϣ�������ֳ�������ɽ��AE�ij��ȣ����ο����ݣ� 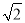 ��1.41�������ȷ��0.1�ף�
��1.41�������ȷ��0.1�ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ�ij���2018����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ������
��3�֣���ͼ���ھ���ABCD�У�AD=2��CD=1������AC���ԶԽ���ACΪ�ߣ�����ʱ�뷽��������ABCD�����ƾ���AB1C1C��������AC1���ԶԽ���AC1Ϊ��������AB1C1C�����ƾ���AB2C2C1�������������˹��ɼ�����ȥ�������ABnCnCn-1�����Ϊ ��
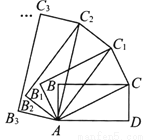
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ�ij���2018����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ���ѡ��
��ͼ���ڡ�ABC�У�DE��BC����ADE=��EFC��AD��BD=5��3��CF=6����DE�ij�Ϊ�� ��
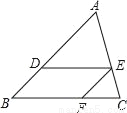
A. 6 B. 8 C. 10 D. 12
C ����������DE��BC�� ���ADE=��B����AED=��C�� �֡ߡ�ADE=��EFC�� ���B=��EFC����ADE�ס�EFC�� ��BD��EF���� ���ı���BFED��ƽ���ı��Σ� ��BD=EF�� �࣬��ã�DE=10. ��ѡC.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ�����ѧ���꼶�ϲ�5.3Ӧ��һԪһ�η���--ˮ�����˿�ʱ��ϰ���������� ���ͣ������
�������С���ڼض���28�ˣ��ҵض���15�ˣ������ֵ���29�ˣ������ڼ��������ضΣ�Ҫ������ض��������ҵض�������2������Ӧ�����ضκ��ҵضθ������ˣ�
Ӧ�����ض�20�ˣ�������ҵض�9�� ���������������� ��Ӧ�����ض�x�ˣ�������ҵضΣ�29-x����-----1�� ��������� 28+x=2��15+29-x�� ------2�� ��� x=20 -------2�� �����飬�������� ���� 29-x=9 ------1�� ��Ӧ�����ض�20�ˣ�������ҵض�9�� --------1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ�����ѧ���꼶�ϲ�5.3Ӧ��һԪһ�η���--ˮ�����˿�ʱ��ϰ���������� ���ͣ���ѡ��
ij������ǿ���ܴ�ʩ��ȥ���°������ϰ�����ȣ���ƽ���õ�������2000�ȣ�ȫ���õ���15��ȣ�������ϰ���ÿ��ƽ���õ�x�ȣ������з�����ȷ���ǣ� ��
A. 6x��6��x��2000����150000
B. 6x��6��x��2000����150000
C. 6x��6��x��2000����15
D. 6x��6��x��2000����15
A ��������������������ϰ���ÿ��ƽ���õ�x�ȣ����°���ÿ��ƽ���õ�Ϊ��x��2000���ȣ�����ȫ���õ���15��ȣ��з��̼��ɣ� �������� ���ϰ���ÿ��ƽ���õ�x�ȣ����°���ÿ��ƽ���õ�Ϊ��x��2000���ȣ� ������ã�6x+6��x��2000��=150000�� ��ѡA���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰���꼶�ϲ���ѧ 22.3ʵ����������κ�����3������ ���ͣ������
�����������100�Ŵ�λ��ÿ��ÿ���շ�10Ԫ���ʹ���ȫ���������ÿ��ÿ���շ����2Ԫ���������λ����10�ţ���ÿ��ÿ���շ������2Ԫ���������λ�ټ���10�ţ���ÿ���2Ԫ�����ֱ仯�����仯��ȥ��ÿ��ÿ�����____Ԫ�ɻ��������
4Ԫ��6Ԫ �������������������ÿ��ÿ�����xԪ��ÿ������ΪW����W=(10+x)(100-5x)= �����ݺ�������ʽ��֪�������5Ԫʱ�����������ÿ����߶���2Ԫ����ÿ�����4Ԫ��6Ԫʱ���Ի����������鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com