练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    抗洪救灾小组在甲地段有28人，乙地段有15人，现在又调来29人，分配在甲乙两个地段，要求调配后甲地段人数是乙地段人数的2倍，求应调至甲地段和乙地段各多少人？

    应调至甲地段20人，则调至乙地段9人 【解析】【解析】 设应调至甲地段x人，则调至乙地段（29-x）人-----1分 根据题意得 28+x=2（15+29-x） ------2分 解得 x=20 -------2分 经检验，符合题意 所以 29-x=9 ------1分 答：应调至甲地段20人，则调至乙地段9人 --------1分
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：天津武清区数学试卷八年级《11.3 多边形及其内角和》同步测试 题型：解答题

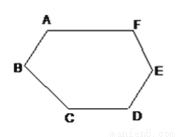
    如图,一个六边形的六个内角都是120°,AB=1,BC=CD=3,DE=2,求该六边形的周长.

    15 【解析】： 试题分析：凸六边形ABCDEF，并不是一规则的六边形，但六个角都是120°，所以通过适当的向外作延长线，可得到等边三角形，进而求解．

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册 22.3 二次函数的应用 同步测试 题型：单选题

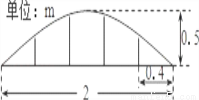
    某公园草坪的防护栏由100段形状相同的抛物线形构件组成，为了牢固起见，每段护栏需要间距0.4m加设一根不锈钢的支柱，防护栏的最高点距底部0.5m（如图），则这条防护栏需要不锈钢支柱的总长度至少为（　　）

    A. 50m B. 100m C. 160m D. 200m

    C 【解析】分析：根据所建坐标系特点可设解析式为y=ax2+c的形式，结合图象易求B点和C点坐标，代入解析式解方程组求出a，c的值得解析式；再根据对称性求B3、B4的纵坐标后再求出总长度． 解答：【解析】 （1）由题意得B（0，0.5）、C（1，0） 设抛物线的解析式为：y=ax2+c 代入得 a=-c= ∴解析式为：y=-x2+ （2）当x=0.2时y=...

    查看答案和解析>>

    科目：初中数学 来源：山东省聊城市2018届九年级上学期期中考试数学试卷 题型：单选题

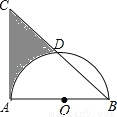
    如图，等腰直角△ABC中，AB=AC=8，以AB为直径的半圆O交斜边BC于D，则阴影部分面积为（结果保留π）（ ）

    A. 16 B. 24-4π C. 32-4π D. 32-8π

    B 【解析】试题分析：连接AD，因为△ABC是等腰直角三角形，故∠ABD=45°，再由AB是圆的直径得出∠ADB=90°，故△ABD也是等腰直角三角形，所以，S阴影=S△ABC-S△ABD-S弓形AD由此可得出结论． 【解析】 连接AD，OD， ∵等腰直角△ABC中， ∴∠ABD=45°. ∵AB是圆的直径， ∴∠ADB=90°， ∴△ABD也是等腰直角...

    查看答案和解析>>

    科目：初中数学 来源：山东省聊城市2018届九年级上学期期中考试数学试卷 题型：单选题

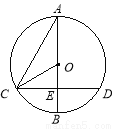
    如图，⊙O的直径AB与弦CD（不是直径）交于点E，且CE=DE，∠A=30°，OC = 4，那么CD的长为

    A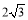． B．4 C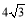． D．8

    C 【解析】 试题分析：因为CE=DE，AB是⊙O的直径，所以CD AB, 又∠A=30°，OA=OC=4,所以∠COE=60°，所以在Rt△COE中，CE=OCsin60°=4×=2，所以CD=2CE=,故选：C.

    查看答案和解析>>

    科目：初中数学 来源：北师大版数学七年级上册5.3应用一元一次方程--水箱变高了课时练习（含解析） 题型：填空题

    一台电脑的进价为2000元，原标价为3000元，现打折销售，要使利润率保持20%，那么需要在原标价的基础上打几折？设需要打x折．可列方程为______．

    3000×＝2000（1＋20%）． 【解析】等量关系:售价=进价+进价×利润率,售价=标价×折扣,设需要打x折,根据题意可列出方程为: 3000×=2000（1＋20%）,故答案为: 3000×=2000（1＋20%）.

    查看答案和解析>>

    科目：初中数学 来源：北师大版数学七年级上册5.3应用一元一次方程--水箱变高了课时练习（含解析） 题型：单选题

    甲、乙两班共有98人，若从甲班调3人到乙班，那么两班人数正好相等．设甲班原有人数是x人，可列出方程（　　）

    A. 98+x=x﹣3 B. 98﹣x=x﹣3 C. （98﹣x）+3=x D. （98﹣x）+3=x﹣3

    D 【解析】试题分析：设甲班原有人数是x人，根据甲、乙两班共有98人，若从甲班调3人到乙班，那么两班人数正好相等可列出方程． 【解析】 设甲班原有人数是x人， （98﹣x）+3=x﹣3． 故选：D．

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 第23章小结与复习 测试 题型：单选题

    下列各图中，图形甲变成图形乙，既能用平移，又能用旋转的是(　C　)

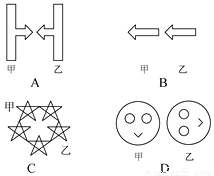
    A. A B. B C. C D. D

    C 【解析】试题分析：A只能通过旋转180°得到；B只能通过平移得到；D只能通过旋转得到；C能用平移，又能用旋转得到，故选C.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年人教八年级数学上册 第14章 章末综合检测 题型：解答题

    下面是某同学对多项式（x2-4x+2）（x2-4x+6）+4因式分解的过程.

    【解析】
    设x2-4x=y，

    则原式=（y+2）（y+6）+4（第一步）

    =y2+8y+16（第二步）

    =（y+4）2（第三步）

    =（x2-4x+4）2（第四步）

    解答下列问题：

    （1）该同学第二步到第三步运用了因式分解的方法是（ ）

    A.提取公因式 B.平方差公式 C.两数和的完全平方公式 D.两数差的完全平方公式

    （2）该同学因式分解的结果是否彻底？（填“彻底”或“不彻底”）.若不彻底，请直接写出因式分解的最后结果；

    （3）请你模仿以上方法尝试对多项式（x2-2x）（x2-2x+2）+1进行因式分解.

    【答案】（1）C；（2）不彻底，（x-2）4；（3）（x-1）4.

    【解析】试题分析：（1）从二步到第三步运用了完全平方和公式；（2）x2-4x+4可运用完全平方差公式因式分解；（3）设x2-2x=y，将（x2-2x）（x2-2x+2）+1变形成y（y+2）+1的形式，再进行因式分解；

    试题解析：

    （1）运用了C，两数和的完全平方公式；

    （2）不彻底；

    （x2-4x+4）2＝（x-2）4

    （3）设x2-2x=y．

    （x2-2x）（x2-2x+2）+1

    =y（y+2）+1

    =y2+2y+1

    =（y+1）2…………………………7分

    =（x2-2x+1）2

    =（x-1）4．

    【题型】解答题
    【结束】
    24

    乘法公式的探究及应用.

    探究问题

    图1是一张长方形纸条，将其剪成长短两条后刚好能拼成图2.

    （1） （2）

    （1）图1中长方形纸条的面积可表示为_______（写成多项式乘法的形式）.

    （2）拼成的图2阴影部分的面积可表示为________（写成两数平方差的形式）.

    （3）比较两图阴影部分的面积，可以得到乘法公式：____.

    结论运用

    （4）运用所得的公式计算：

    =________； =________.

    拓展运用：

    （5）计算：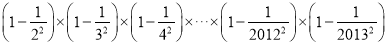

    （1）（a+b）·（a-b）；（2）a2-b2；（3）（a+b）（a-b）=a2-b2；（4）4x2-y2， ；（5） 【解析】试题分析：（1）（2）（3）利用面积证明了平方差公式. (4)应用完全平方公式. (5)利用平方差公式，把每一项展开并计算，约分就可以得到结果. 试题解析： 【解析】 （1）图14-5（1）是一张长方形纸条，将其剪成长短两条后刚好能拼成图1...

    查看答案和解析>>

    同步练习册答案