请把下面证明过程补充完整：
已知：如图，∠ADC=∠ABC，BE、DF分别平分∠ABC、∠ADC，且∠1=∠2．
求证：∠A=∠C．
证明：∵BE、DF分别平分∠ABC、∠ADC(已知)，
∴∠1=
∠ABC，∠3=
∠ADC(角平分线定义)．
∵∠ABC=∠ADC(已知)，
∴∠1=∠3(等量代换)，
∵∠1=∠2(已知)，
∴∠2=∠3(等量代换)．
∴_____∥_____ (___ __)．
∴∠A+∠_____=180°，∠C+∠_____=180°(___ __)．
∴∠A=∠C(___ __)．
寒假天地重庆出版社系列答案科目：初中数学 来源：江苏省盐城市2017-2018学年八年级下学期期中考试数学试卷 题型：解答题
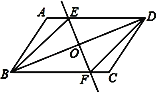
已知：如图，在平行四边形ABCD中，O为对角线BD的中点，过点O的直线EF分别交AD，BC于E，F两点，连结BE，DF．
（1）求证：△DOE≌△BOF．
（2）当∠DOE等于多少度时，四边形BFDE为菱形？请说明理由．
查看答案和解析>>
科目：初中数学 来源：山东蒙阴县2017-2018学年度下学期七年级期中考试数学试卷 题型：解答题
（1）问题发现
如图①，直线AB∥CD，E是AB与AD之间的一点，连接BE，CE，可以发现∠B+∠C=∠BEC．
请把下面的证明过程补充完整：
证明：过点E作EF∥AB，
∵AB∥DC（已知），EF∥AB（辅助线的作法），
∴EF∥DC
∴∠C= ．
∵EF∥AB，∴∠B= ，
∴∠B+∠C= .
即∠B+∠C=∠BEC．
（2）拓展探究
如果点E运动到图②所示的位置，其他条件不变，求证：∠B+∠C=360°﹣∠BEC．
（3）解决问题
如图③，AB∥DC，∠C=120°，∠AEC=80°，则∠A= ．（直接写出结论，不用写计算过程）
查看答案和解析>>
科目：初中数学 来源：山东蒙阴县2017-2018学年度下学期七年级期中考试数学试卷 题型：单选题
如图，把一块直角三角板的直角顶点放在直尺的一边上，如果∠1=36°，那么∠2的度数为
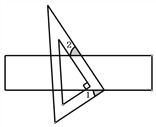
A. 44° B. 54° C. 60° D. 36°
查看答案和解析>>
科目：初中数学 来源：广东省汕头市2018届九年级中考数学模拟试卷 题型：填空题
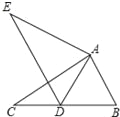
如图，在△ABC中，AB=2，BC=3.5，∠B=60°，将△ABC绕点A按顺时针旋转一定角度得到△ADE，当点B的对应点D恰好落在BC边上时，则CD的长为_____．
查看答案和解析>>
科目：初中数学 来源：贵州省遵义市2018年中考数学模拟试卷 题型：解答题
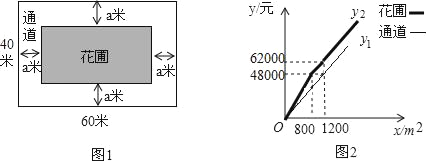
如图1，为美化校园环境，某校计划在一块长为60米，宽为40米的长方形空地上修建一个长方形花圃，并将花圃四周余下的空地修建成同样宽的通道，设通道宽为a米．
（1）用含a的式子表示花圃的面积．
（2）如果通道所占面积是整个长方形空地面积的
，求出此时通道的宽．
（3）已知某园林公司修建通道、花圃的造价y1（元）、y2（元）与修建面积x（m2）之间的函数关系如图2所示，如果学校决定由该公司承建此项目，并要求修建的通道的宽度不少于2米且不超过10米，那么通道宽为多少时，修建的通道和花圃的总造价最低，最低总造价为多少元？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
有意义，则x的取值范围是__；
的点表示的数是____.