
已知,抛物线y=ax2+ax+b(a≠0)与直线y=2x+m有一个公共点M(1,0),且a<b.
(1)求b与a的关系式和抛物线的顶点D坐标(用a的代数式表示);
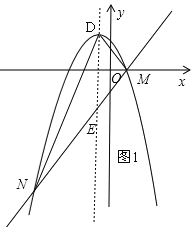
(2)直线与抛物线的另外一个交点记为N,求△DMN的面积与a的关系式;
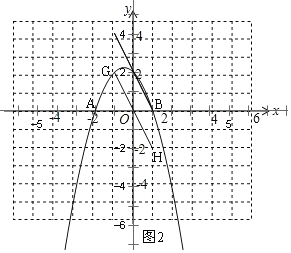
(3)a=﹣1时,直线y=﹣2x与抛物线在第二象限交于点G,点G、H关于原点对称,现将线段GH沿y轴向上平移t个单位(t>0),若线段GH与抛物线有两个不同的公共点,试求t的取值范围.
【答案】(1)b=﹣2a,顶点D的坐标为(﹣ ,﹣
,﹣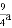 );(2)
);(2)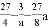 ;(3) 2≤t<
;(3) 2≤t< .
.
【解析】试题分析:(1)把M点坐标代入抛物线解析式可得到b与a的关系,可用a表示出抛物线解析式,化为顶点式可求得其顶点D的坐标;
(2)把点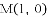 代入直线解析式可先求得m的值,联立直线与抛物线解析式,消去y,可得到关于x的一元二次方程,可求得另一交点N的坐标,根据a<b,判断a<0,确定D、M、N的位置,画图1,根据面积和可得
代入直线解析式可先求得m的值,联立直线与抛物线解析式,消去y,可得到关于x的一元二次方程,可求得另一交点N的坐标,根据a<b,判断a<0,确定D、M、N的位置,画图1,根据面积和可得
(3)先根据a的值确定抛物线的解析式,画出图2,先联立方程组可求得当GH与抛物线只有一个公共点时,t的值,再确定当线段一个端点在抛物线上时,t的值,可得:线段GH与抛物线有两个不同的公共点时t的取值范围.
试题解析:(1)∵抛物线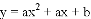 有一个公共点M(1,0),
有一个公共点M(1,0),
∴a+a+b=0,即b=?2a,
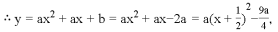
∴抛物线顶点D的坐标为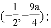
(2)∵直线y=2x+m经过点M(1,0),
∴0=2×1+m,解得m=?2,
∴y=2x?2,
则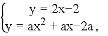
得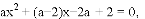
∴(x?1)(ax+2a?2)=0,
解得x=1或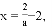
∴N点坐标为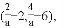
∵a<b,即a<?2a,
∴a<0,
如图1,设抛物线对称轴交直线于点E,
∵抛物线对称轴为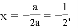
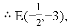
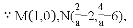
设△DMN的面积为S,
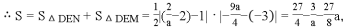
(3)当a=?1时,
抛物线的解析式为: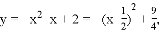
有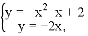
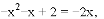
解得:
∴G(?1,2),
∵点G、H关于原点对称,
∴H(1,?2),
设直线GH平移后的解析式为:y=?2x+t,
?x2?x+2=?2x+t,
x2?x?2+t=0,
△=1?4(t?2)=0,
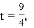 当点H平移后落在抛物线上时,坐标为(1,0),
当点H平移后落在抛物线上时,坐标为(1,0),
把(1,0)代入y=?2x+t,
t=2,
∴当线段GH与抛物线有两个不同的公共点,t的取值范围是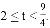
【题型】解答题
【结束】
24
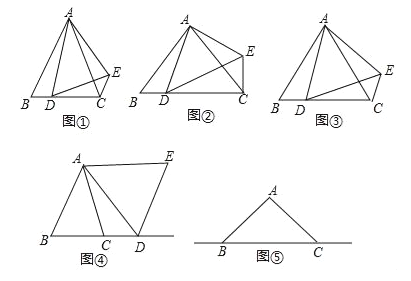
在△ABC中,AB=AC,点D是直线BC上的一点(不与B,C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE,设∠BAC=α,∠BCE=β.
(1)如图①,当点D在线段BC上,如果α=60°,β=120°;
如图②,当点D在线段BC上,如果α=90°,β=90°
如图③,当点D在线段BC上,如果α,β之间有什么样的关系?请直接写出.
(2)如图④,当点D在射线BC上,(1)中结论是否成立?请说明理由.
(3)如图⑤,当点D在射线CB上,且在线段BC外,(1)中结论是否成立?若不成立,请直接写出你认为正确的结论.
科目:初中数学 来源:安徽省合肥市2018届九年级中考模拟测试 数学试卷 题型:解答题
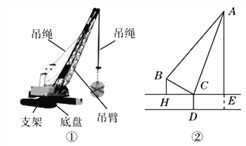
如图①,②分别是某吊车在吊一物品时的实物图与示意图,已知吊车底盘CD的高度为2米,支架BC的长为4米,且与地面成30°角. 吊绳AB与支架BC的夹角为80°,吊臂AC与地面成70°角,求吊车的吊臂顶端A距地面的高度是多少米?(精确到0.1米. 参考数据:sin10°=cos80°≈0.17,cos10°=sin80°≈0.98,sin20°=cos70°≈0.34,tan70°≈2.75,sin70°≈0.94)
查看答案和解析>>
科目:初中数学 来源:四川省内江市县2018届九年级中考一模试卷数学试卷 题型:单选题
在半径等于5cm的圆内有长为5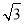 cm的弦,则此弦所对的圆周角为( )
cm的弦,则此弦所对的圆周角为( )
A.120° B.30°或120°
C.60° D.60°或120°
查看答案和解析>>
科目:初中数学 来源:四川省内江市县2018届九年级中考一模试卷数学试卷 题型:单选题
在平面直角坐标系中,将抛物线y=(x+1)2向右平移2个单位,再向下平移4个单位,得到的抛物线解析式是( )
A. y=(x﹣2)2﹣4 B. y=(x﹣1)2﹣4 C. y=(x﹣2)2﹣3 D. y=(x﹣1)2﹣3
查看答案和解析>>
科目:初中数学 来源:内蒙古鄂尔多斯市2018届九年级中考数学模拟试卷(一) 题型:解答题
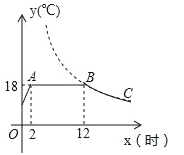
某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光明且温度为18℃的条件下生长最快的新品种,如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线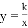 的一部分.请根据图中信息解答下列问题:
的一部分.请根据图中信息解答下列问题:
(1)恒温系统在这天保持大棚内温度18℃的时间有多少小时?
(2)求k的值;
(3)当x=15时,大棚内的温度约为多少度?
查看答案和解析>>
科目:初中数学 来源:河南省2018届九年级中考数学仿真试卷(一) 题型:解答题
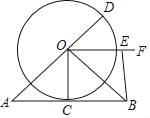
如图,在△ABO中,OA=OB,C是边AB的中点,以O为圆心的圆过点C,连接OC,AO延长线交⊙O于点D,OF是∠DOB的平分线,E为OF上一点,连接BE.
(1)求证:AB与⊙O相切;
(2)①当∠OEB=_____时,四边形OCBE为矩形;
②在①的条件下,若AB=4,则OA=_____时,四边形OCBE为正方形?
查看答案和解析>>
科目:初中数学 来源:2017-2018邗江区九年级中考数学第一次模拟考试试卷 题型:单选题
一组数据:1、2、2、3,若添加一个数据2,则发生变化的统计量是( )
A. 平均数 B. 中位数 C. 众数 D. 方差
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com