
如图,点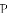
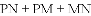
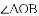
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:初中数学 来源:2017年广西南宁市兴宁区英华学校中考数学模拟试卷 题型:单选题
若关于x的一元二次方程方程(k﹣1)x2+4x+1=0有实数根,则k的取值范围是( )
A. k<5 B. k≥5,且k≠1 C. k≤5,且k≠1 D. k>5
C 【解析】试题解析:∵关于x的一元二次方程方程有实数根, ∴ 解得: 且k≠1. 故选C.查看答案和解析>>
科目:初中数学 来源:福建省三明市大田县2017-2018学年八年级上期末模拟数学试卷 题型:解答题
如图:△ABC中,D为BC的中点,DE⊥BC交∠BAC的平分线AE于E,EG⊥AB于G,EF⊥AC交AC的延长线于F,BG与CF的大小关系如何?并证明你的结论.
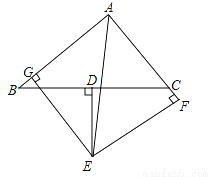
查看答案和解析>>
科目:初中数学 来源:福建省三明市大田县2017-2018学年八年级上期末模拟数学试卷 题型:单选题
如果每盒钢笔有10支,售价25元,那么购买钢笔的总钱数y(元)与支数x之间的关系式为( )
A. y=10x B. y=25x C. y=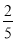 x D. y=
x D. y=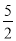 x
x
查看答案和解析>>
科目:初中数学 来源:2017-2018学年苏州市第一学期八年级数学期末复习综合检测卷 题型:解答题
如图,在四边形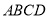 中,
中, 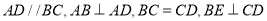 ,垂足为
,垂足为 .
.
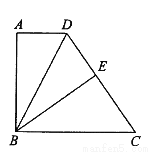
(1)求证: 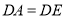 .
.
(2)若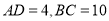 ,求
,求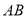 的长.
的长.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年苏州市第一学期八年级数学期末复习综合检测卷 题型:填空题
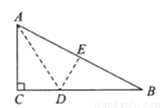
如图,有一块直角三角形纸片,两直角边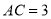 cm,
cm, 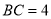 cm,现将直角边
cm,现将直角边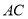 沿直线
沿直线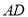 折叠,使它落在斜边
折叠,使它落在斜边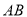 上,且与
上,且与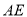 重合,则
重合,则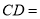 _________.
_________.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年苏州市第一学期八年级数学期末复习综合检测卷 题型:单选题
如图,如果把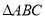 的顶点
的顶点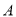 先向下平移3格,再向左平移1格到达
先向下平移3格,再向左平移1格到达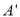 点,连接
点,连接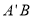 ,那么线段
,那么线段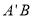 与线段
与线段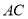 的关系是( )
的关系是( )
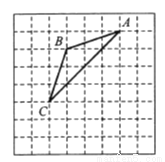
A. 垂直 B. 相等 C. 平分 D. 平分且垂直
D 【解析】试题解析:如图,将点A先向下平移3格,再向左平移1格到达A′点,连接A′B,与线段AC交于点O. ∵A′O=OB=,AO=OC=2, ∴线段A′B与线段AC互相平分, 又∵∠AOA′=45°+45°=90°, ∴A′B⊥AC, ∴线段A′B与线段AC互相垂直平分. 故选D.查看答案和解析>>
科目:初中数学 来源:山东省2017-2018学年八年级上学期第二次月考数学试卷 题型:单选题
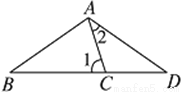
如图,AD=AB=BC,那么∠1和∠2之间的关系是 ( )
A. ∠1=∠2
B. 2∠1+∠2=180°
C. ∠1+3∠2=180°
D. 3∠1-∠2=180°
D 【解析】试题分析:根据题意得:∠1=∠2+∠D,∠B=∠D,∠1=∠BAC,根据△ABD的内角和可得:∠D=(180-∠BAC-∠2)÷2=(180-∠1-∠2)÷2,∴∠1=∠2+(180-∠1-∠2)÷2,∴3∠1-∠2=180°.查看答案和解析>>
科目:初中数学 来源:2017年甘肃省白银市中考数学二模试卷 题型:解答题
已知关于x的一元二次方程(a+c)x2+2bx+(a﹣c)=0,其中a、b、c分别为△ABC三边的长.
(1)如果x=﹣1是方程的根,试判断△ABC的形状,并说明理由;
(2)如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由;
(3)如果△ABC是等边三角形,试求这个一元二次方程的根.
【解析】 (1)△ABC是等腰三角形,理由见解析; (2)△ABC是直角三角形,理由见解析; (3)x1=0,x2=﹣1. 【解析】试题分析:(1)直接将x=-1代入得出关于a,b的等式,进而得出a=b,即可判断△ABC的形状; (2)利用根的判别式进而得出关于a,b,c的等式,进而判断△ABC的形状; (3)利用△ABC是等边三角形,则a=b=c,进而代入方程求出...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com