练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    下面是“作一个30°角”的尺规作图过程．

    请回答：该尺规作图的依据是______________________________________________________．

    三条边相等的三角形是等边三角形，等边三角形的三个内角都是60°，一条弧所对的圆周角是它所对圆心角的一半；或：直径所对的圆周角为直角，三条边相等的三角形是等边三角形，等边三角形的三个内角都是60°，直角三角形两个锐角互余；或：直径所对的圆周角为直角， ， 为锐角， . 【解析】连接OD,CD,因为OC=OC=CD,所以OCD是等边三角形，∠A= 三条边相等的三角形是等边三角形，等边三角形...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：北京市丰台区2017-2018学年七年级上学期期末考试数学试卷（WORD版） 题型：解答题

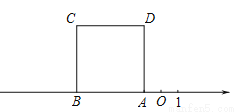
    如图，正方形ABCD的边AB在数轴上，数轴上点A表示的数为-1，正方形ABCD的面积为16．

    （1）数轴上点B表示的数为 ；

    （2）将正方形ABCD沿数轴水平移动，移动后的正方形记为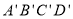，移动后的正方形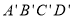与原正方形ABCD重叠部分的面积记为S．

    ① 当S =4时，画出图形，并求出数轴上点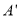表示的数；

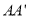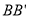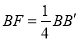    ② 设正方形ABCD的移动速度为每秒2个单位长度，点E为线段的中点，点F在线段上，且. 经过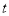秒后，点E，F所表示的数互为相反数，直接写出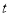的值．

    （1）－5；（2）– 4或2；（3）t=4． 【解析】试题分析：(1)、根据正方形的面积得出AB=4，根据点A所表示的数得出点B所表示的数；(2)、①、根据题意得出矩形的一边长为4，要使面积为4，则另一边长为1，然后根据向左移动和向右移动两种情况分别画出图形得出答案；②、用含t的代数式分别表示出点E和点F所表示的数，然后根据互为相反数的两个数的和为零列出方程得出答案． 试题解析：【解析...

    查看答案和解析>>

    科目：初中数学 来源：内蒙古乌兰察布分校2017-2018学年七年级上学期期末考试数学试卷 题型：填空题

    若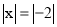，则 ______ ．

    ±2 【解析】试题分析：因为|x|＝|－2|， 所以|x|＝2， 所以x＝±2． 故答案为±2．

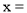    查看答案和解析>>

    科目：初中数学 来源：北京市海淀区2018届九年级上学期期末考试数学试卷 题型：解答题

    在△ABC中，∠A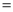90°，AB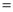AC．

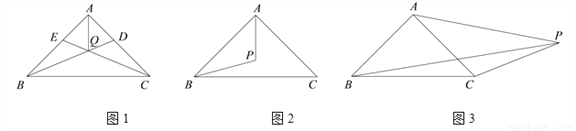
    （1）如图1，△ABC的角平分线BD，CE交于点Q，请判断“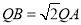”是否正确：________（填“是”或“否”）；

    （2）点P是△ABC所在平面内的一点，连接PA，PB，且PB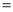 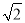PA．

    ①如图2，点P在△ABC内，∠ABP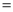30°，求∠PAB的大小；

    ②如图3，点P在△ABC外，连接PC，设∠APC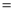α，∠BPC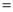β，用等式表示α，β之间的数量关系，并证明你的结论．

    （1）否；（2）①45°；②． 【解析】试题分析： （1）如图4，把△AQC顺时针旋转90°得到△AQ1B，连接QQ1，则由题意易得QQ1=AQ，由已知条件可证∠BQ1Q∠Q1BQ，从而可得BQQQ1=AQ； （2）①如图5，过点PD⊥AB于点，结合∠ABP=30°可得PD=PB，结合PB=PA可得PD=PA，由此即可得到sin∠PAB=，结合∠PAB是锐角即可得到∠PAB=45...

    查看答案和解析>>

    科目：初中数学 来源：北京市海淀区2018届九年级上学期期末考试数学试卷 题型：解答题

    如图，在△ABC中，∠B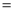90°，AB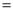4，BC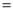2，以AC为边作△ACE，∠ACE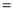90°，AC=CE，延长BC至点D，使CD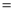5，连接DE．求证：△ABC∽△CED．

    证明见解析 【解析】试题分析： 由已知易证∠BAC=∠ECD，在Rt△ABC中由已知可得AC==CE， 结合AB=4，CD=5，可证得，由此即可由“两边对应成比例，且夹角相等的两三角形相似”得到△ABC∽△CED． 试题解析： ∵ ∠B=90°，AB=4，BC=2， ∴. ∵ CE=AC， ∴. ∵ CD=5， ∴. ∵ ∠B=90°，∠...

    查看答案和解析>>

    科目：初中数学 来源：北京市海淀区2018届九年级上学期期末考试数学试卷 题型：填空题

    若一个反比例函数图象的每一支上，y随x的增大而减小，则此反比例函数表达式可以是__________．（写出一个即可）

    （答案不唯一） 【解析】∵反比例函数图象的每一支上，y随x的增大而减小， ∴该反比例函数中，常数，如等（答案不唯一，只要即可）.

    查看答案和解析>>

    科目：初中数学 来源：北京市海淀区2018届九年级上学期期末考试数学试卷 题型：单选题

    如图，将△ABC绕点A逆时针旋转100°，得到△ADE．若点D在线段BC的延长线上，则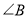的大小为（　　）

    A. 30° B. 40° C. 50° D. 60°

    B 【解析】∵△ADE是由△ABC绕点A旋转100°得到的， ∴∠BAD=100°，AD=AB， ∵点D在BC的延长线上， ∴∠B=∠ADB=. 故选B.

    查看答案和解析>>

    科目：初中数学 来源：2018年1月北京市海淀区初三上数学期末试卷 题型：填空题

    在同车道行驶的机动车，后车应当与前车保持足以采取紧急制动措施的安全距离．如图，在一个路口，一辆长为10m的大巴车遇红灯后停在距交通信号灯20m的停止线处，小张驾驶一辆小轿车跟随大巴车行驶．设小张距大巴车尾x m，若大巴车车顶高于小张的水平视线0.8m，红灯下沿高于小张的水平视线3.2m，若小张能看到整个红灯，则x的最小值为__________．

    10 【解析】如图，由题意可知，CD∥AB， ∴△OCD∽△OAB， ∴，即，解得. 故答案为： .

    查看答案和解析>>

    科目：初中数学 来源：云南省2016-2017学年八年级上学期期末考试数学试卷 题型：解答题

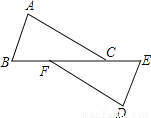
    如图点B、F、C、E在一直线上，FB＝CE，AB∥ED，AC∥FD。求证：AB＝DE．

    见解析 【解析】试题分析：利用公共边得到BC=EF,再利用平行得到角相等，利用ASA证明三角形全等，可得AB＝DE． 试题解析： 证明：在△ABC和△DEF中, ∵ FB=CE, ∴ FB+FC=CE+FC, 即BC=EF, 又∵AB∥ED，AC∥FD, ∴∠B=∠E，∠ACB=∠DFE, ∴△ABC≌△DEF（ASA）.

    查看答案和解析>>

    同步练习册答案