
在Rt△ABC中,∠C=90°,AB=4,AC=1,则cosB的值为( )
A. 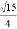 B.
B.  C.
C. 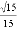 D.
D. 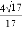
 口算能手系列答案
口算能手系列答案科目:初中数学 来源:广东省江门市江海区五校2017-2018学年七年级上学期期末联考数学试卷 题型:解答题
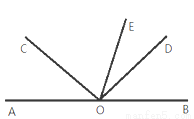
如图,点A、O、B在同一条直线上,∠AOC=∠BOD,OE是∠BOC的平分线.
(1)若∠AOC=46°,求∠DOE的度数;
(2)若∠DOE=30°,求∠AOC的度数.
查看答案和解析>>
科目:初中数学 来源:2017年陕西省西安市中考数学模拟试卷 题型:单选题
已知实数x满足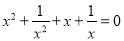 ,那么
,那么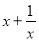 的值是( )
的值是( )
A. 1或﹣2 B. ﹣1或2 C. 1 D. ﹣2
D 【解析】∵x2+=0 ∴(x+)2-2+x+=0, ∴[(x+)+2][(x+)﹣1]=0, ∴x+=1或﹣2. ∵x+=1无解, ∴x+=﹣2. 故选:D.查看答案和解析>>
科目:初中数学 来源:2017学年第一学期上海(闵行区)九年级数学质量调研试卷 题型:填空题
半径分别为20cm与15cm的⊙O1与⊙O2相交于A、B两点,如果公共弦AB的长为24cm,那么圆心距O1O2的长为 cm.
25或7 【解析】试题解析:∵两个圆相交,公共弦长为24cm, ∴连接两圆的圆心,连心线的一半,半径和公共弦的一半构成直角三角形。 当两圆的圆心在公共弦的两侧时,解得圆心距为: 当两圆的圆心在公共弦的同侧时,解得公共弦长为: 故答案为:25或7.查看答案和解析>>
科目:初中数学 来源:2017学年第一学期上海(闵行区)九年级数学质量调研试卷 题型:填空题
已知两个相似三角形的相似比为2︰5,其中较小的三角形面积是 ,那么另一个三角形的面积为 .
,那么另一个三角形的面积为 .
查看答案和解析>>
科目:初中数学 来源:陕西省宝鸡市2017-2018学年八年级上学期期中考试数学试卷 题型:解答题
如图,一次函数y=-x+m的图象和y轴交于点B,与正比例函数y=x图象交于点P (2,n).
(1)求m和n的值;
(2)求△POB的面积.
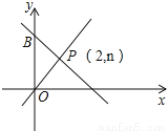
查看答案和解析>>
科目:初中数学 来源:陕西省宝鸡市2017-2018学年八年级上学期期中考试数学试卷 题型:填空题
如图,在三角形纸片ABC中,∠C=90°,AC=18,将∠A沿DE折叠,使点A与点B重合,折痕和AC交于点E,EC=5,则BC的长为______.
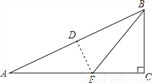
查看答案和解析>>
科目:初中数学 来源:2017学年度第一学期上海(杨浦区)期末考试初三数学试卷 题型:解答题
如图是某路灯在铅垂面内的示意图,灯柱BC的高为10米,灯柱BC与灯杆AB的夹角为120°.路灯采用锥形灯罩,在地面上的照射区域DE的长为13.3米,从D、E两处测得路灯A的仰角分别为α和45°,且tanα=6.求灯杆AB的长度.
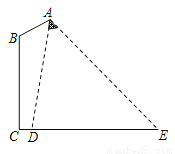
查看答案和解析>>
科目:初中数学 来源:内蒙古赤峰市宁城县2018届九年级上学期期末数学试卷 题型:单选题
在△ABC中,DE∥BC,若AD=1,DB=2,则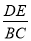 的值为( )
的值为( )
A. 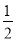 B.
B. 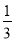 C.
C. 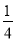 D.
D. 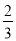
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com