
有一位旅客携带了30kg重的行李从上海乘飞机去北京,按民航总局规定:旅客最多可免费携带20kg重的行李,超重部分每千克按飞机票价格1.5%购买行李票,现该旅客购买了180元的行李票,则飞机票价格应是多少元?
飞机票价格应是1200元. 【解析】试题分析:设飞机票价格应是x元,根据该旅客购买了180元的行李票,列方程求解. 试题解析:【解析】 设飞机票价格应是x元,由题意得:(30﹣20)×1.5% x=180,解之得:x=1200. 答:飞机票价格应是1200元. 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源:天津武清区数学试卷八年级《11.3 多边形及其内角和》同步测试 题型:解答题
小华从点A出发向前走10米,向右转36°,然后继续向前走10米,再向右转36°,他以同样的方法继续走下去,他能回到点A吗?若能,当他走回点A时共走了多少米?若不能,写出理由.
可以走回到A点,共走100米 【解析】试题分析:他要想回到原点需要走成正多边形,根据多边形的外角和定理求出多边形的边数,从而求出路程. 试题解析:【解析】 根据题意可知,360°÷36°=10,所以他需要转10次才会回到起点,它需要经过10×10=100m才能回到原地. 所以小华能回到点A.当他走回到点A时,共走100m.查看答案和解析>>
科目:初中数学 来源:人教版九年级上册 22.3 二次函数的应用 同步测试 题型:单选题
如图,铅球运动员掷铅球的高度y(m)与水平距离x(m)之间的函数关系式是y=﹣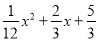 ,则该运动员此次掷铅球的成绩是( )
,则该运动员此次掷铅球的成绩是( )
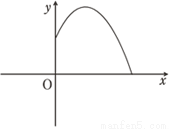
A. 6m B. 12m C. 8m D. 10m
D 【解析】试题分析:根据图示,把y=0代入y=-x2+x+可得:-x2+x+=0,解之得:x1=10,x2=-2.又x>0,解得x=10. 故选D.查看答案和解析>>
科目:初中数学 来源:山东省聊城市2018届九年级上学期期中考试数学试卷 题型:单选题
小明同学将一张圆桌紧靠在矩形屋子的一角,与相邻两面墙相切,她把切点记为A、B,然后,她又在桌子边缘上任取一点P(异于A、B),则∠APB的度数为( )

A. 45° B. 135° C. 45°或135° D. 90°或135°
C 【解析】试题分析:连接OA、OB,则∠MAO=∠MBO=90°即可求得弧AB所对的圆心角的度数,然后分P在优弧和劣弧上两种情况进行讨论,利用圆周角定理即可求解. 【解析】 连接OA、OB,则∠MAO=∠MBO=90°, 又∵∠M=90°, ∴四边形AOBM是矩形。 ∴∠AOB=90°, 当P在AB所对的优弧上时,∠P=∠AOB=45°, 则当P在劣弧...查看答案和解析>>
科目:初中数学 来源:山东省聊城市2018届九年级上学期期中考试数学试卷 题型:单选题
下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则在网格图中的三角形与△ABC相似的是( )
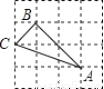
A. 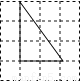 B.
B. 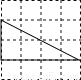 C.
C. 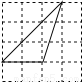 D.
D. 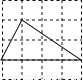
查看答案和解析>>
科目:初中数学 来源:北师大版数学七年级上册5.3应用一元一次方程--水箱变高了课时练习(含解析) 题型:填空题
小明与家人和同学一起到游泳池游泳,买了2张成人票与3张学生票,共付了155元.已知成人票的单价比学生票的单价贵15元,设学生票的单价为x元,可得方程______.
3x+2(x+15)=155 【解析】根据等量关系:2张成人票的价钱+3张学生票的价钱=共付的钱数,设学生票的单价为x元,因为成人票的单价比学生票的单价贵15元,所以成人票的单价为:(x+15)元,根据题意可列出方程为: 3x+2(x+15)=155,故答案为: 3x+2(x+15)=155.查看答案和解析>>
科目:初中数学 来源:北师大版数学七年级上册5.3应用一元一次方程--水箱变高了课时练习(含解析) 题型:单选题
一个饲养场里的鸡的只数与猪的头数之和是70,鸡、猪的腿数之和是196,设鸡的只数是x,依题意列方程为( )
A. 2x+4(70-x)=196
B. 2x+4×70=196
C. 4x+2(70-x)=196
D. 4x+2×70=196
A 【解析】设鸡的只数为x,则猪的头数为(70-x)头,根据鸡,猪的腿数之和是196,可列方程: 2x+4(70-x)=196,故选A.查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 第23章小结与复习 测试 题型:单选题
民间剪纸是中国民间美术形式之一,有着悠久的历史,如图的图案是中心对称图形的是( )

查看答案和解析>>
科目:初中数学 来源:2017-2018学年人教八年级数学上册 第14章 章末综合检测 题型:解答题
(1)先化简,再求值:a(a-2b)+(a+b)2,其中a=-1,b=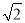 ;
;
(2)若x2-5x=3,求(x-1)(2x-1)-(x+1)2+1的值.
【答案】(1)原式= 2a2+b2=2+2=4;(2)原式=4.
【解析】试题分析:(1)利用完全平方公式展开,化简,代入求值. (2) 利用完全平方公式展开,化简,整体代入求值.
解:(1)原式=a2-2ab+a2+2ab+b2=2a2+b2.
当a=-1,b=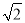 时,原式=2+2=4.
时,原式=2+2=4.
(2)原式=2x2-3x+1-(x2+2x+1)+1=x2-5x+1=3+1=4.
【题型】解答题
【结束】
22
已知化简(x2+px+8)(x2-3x+q)的结果中不含x2项和x3项.
(1)求p,q的值.
(2)x2-2px+3q是否是完全平方式?如果是,请将其分解因式;如果不是,请说明理由.
(1);(2)x2-2px+3q不是完全平方式.理由见解析. 【解析】试题分析:(1)展开,化简,让x2项和x3项系数为0. (2)把(1)中结论代入,不满足完全平方公式. 试题解析: 解:(1)原式=x4+(-3+p)x3+(q-3p+8)x2+(pq-24)x+8q. ∵结果中不含x2项和x3项,∴ 解得 (2)x2-2px+3q不是完全平方式.理由如...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com