
11点整,时钟的分针与夹角是______。
30° 【解析】11点整时时针指向11,分针指向12,所以它们的夹角是30°. 故答案为30°. 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:湖南省2017-2018学年八年级数学上期末复习检测数学试卷 题型:解答题
在创建全国森林城市的活动中,我区一“青年突击队”决定义务整修一条1000米长的绿化带,开工后,附近居民主动参加到义务劳动中,使整修的速度比原计划提高了一倍,结果提前4小时完成任务,问“青年突击队”原计划每小时整修多少米长的绿化带?
原计划每小时整修125米长的绿化带. 【解析】试题分析:设原计划每小时整修x米长的绿化带,根据“计划时间-实际时间=4”这一等量关系列出方程,解方程即可得. 试题解析:设原计划每小时整修x米长的绿化带, 根据题意得: , 解得:x=125, 经检验:x=125是原方程的解, ∴x=125 答:原计划每小时整修125米长的绿化带.查看答案和解析>>
科目:初中数学 来源:湖南省2017-2018学年八年级数学上期末复习检测数学试卷 题型:单选题
已知方程组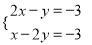 的解为
的解为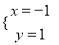 ,则函数y=2x+3与
,则函数y=2x+3与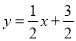 的交点坐标为( )?
的交点坐标为( )?
A. (1,5) B. (-1,1) C. (1,2) D. (4,1)
B 【解析】∵方程组的解为,∴函数y=2x+3与的交点坐标为(-1,1),故选B.查看答案和解析>>
科目:初中数学 来源:2017-2018苏科版南京栖霞区七年级数学上册12月份月考试卷有答案 题型:解答题
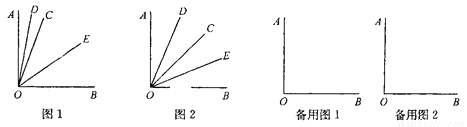
已知∠AOB是一个直角,作射线OC,再分别作∠AOC和∠BOC的平分线OD,OE.
(1) 如图1,当∠BOC=70°时,求∠DOE的度数.
(2) 如图2,当射线OC在∠AOB内绕点O旋转时,∠DOE的大小是否发生变化?说明理由.
(3) 当射线OC在∠AOB外绕点O旋转且∠AOC为钝角时,画出图形,直接写出相应的∠DOE的度数.(不必写出过程)
查看答案和解析>>
科目:初中数学 来源:2017-2018苏科版南京栖霞区七年级数学上册12月份月考试卷有答案 题型:填空题
如图是一个由7个同样大小的小立方体搭成的几何体,请画出这个几何体的主视图、左视图和俯视图.

查看答案和解析>>
科目:初中数学 来源:2017-2018苏科版南京栖霞区七年级数学上册12月份月考试卷有答案 题型:填空题
如果一个几何体的三个视图之一是三角形,这个几何体可能是_______、_______、_______.(写出3个即可).
三棱柱、 三棱锥、 圆锥 【解析】如果俯视图是三角形,则这个几何体可能是三棱锥,如果主视图或左视图是三角形,则这个几何体可能是三棱锥或圆锥. 故答案为 (1). 三棱柱、 (2). 三棱锥、 (3). 圆锥查看答案和解析>>
科目:初中数学 来源:2017-2018苏科版南京栖霞区七年级数学上册12月份月考试卷有答案 题型:单选题
下列图形中,是正方体的表面展开图的是 ( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:湖南省2017-2018学年八年级数学上期末复习检测数学试卷 题型:单选题
如图所示,△ABC中,AB=BC=AC,BD=CE,AD与BE相交于点P,则∠APE的度数是( )
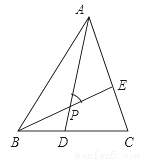
A. 45° B. 55° C. 75° D. 60°
D 【解析】在△ABD和△BCE中, ∴△ABD≌△BCE(SAS), ∴∠BAD=∠CBE, ∵∠APE=∠ABE+∠BAD,∠ABE+∠CBE=60°, ∴∠APE=∠ABC=60°. 故选D.查看答案和解析>>
科目:初中数学 来源:2017年江苏省苏州市中考数学三模试卷 题型:解答题
解方程:  .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com