
如图,在△ABC,P为AB上一点,连结CP,下列条件中不能判定△ACP∽△ABC的是( )
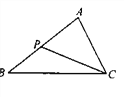
A. ∠ACP=∠B B. ∠APC=∠ACB C. 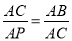 D.
D. 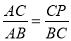
科目:初中数学 来源:广东省东莞市堂星晨学校2017-2018学年八年级5月月查数学试卷 题型:填空题
若三角形三条边的长分别为7,24,25,则这个三角形的最大内角是_______度.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年苏科版八年级下学期数学期末专题复习试卷五 题型:解答题
已知关于x的方程x2-(m+2)x+(2m-1)=0。
(1)求证:方程恒有两个不相等的实数根;
(2)若此方程的一个根是1,请求出方程的另一个根,并求以此两根为边长的直角三角形的周长。
查看答案和解析>>
科目:初中数学 来源:安徽省2017-2018学年度第一学期第三次大联考八年级数学检测卷 题型:解答题
如图所示,□ABCD的对角线AC,BD相交于点O,E、F、G、H分别是OA、OB、OC、OD的中点,那么□ABCD与四边形EFGH是否是位似图形?为什么?
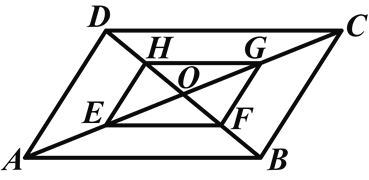
查看答案和解析>>
科目:初中数学 来源:安徽省2017-2018学年度第一学期第三次大联考八年级数学检测卷 题型:单选题
(2015秋•安徽月考)如图,四边形ABCD为正方形,若AB=4,E是AD边上一点(点E与点A、D不重合),BE的中垂线交AB于点M,交DC于点N,设AE=x,BM=y,则y与x的大致图象是( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:江西省等学校招生考试数学试卷 题型:解答题
小贤与小杰在探究某类二次函数问题时,经历了如下过程:
求解体验
(1)已知抛物线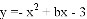 经过点(-1,0),则
经过点(-1,0),则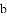
抽象感悟
我们定义:对于抛物线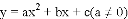 ,以
,以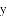
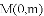
点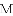
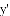
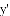
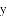
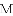
(2)已知抛物线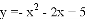 关于点
关于点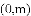
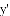
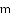
问题解决
(3) 已知抛物线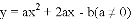
①若抛物线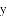
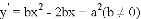 ,两抛物线有两个交点,且恰好是它们的顶点,求
,两抛物线有两个交点,且恰好是它们的顶点,求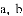
②若抛物线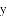
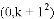 的衍生抛物线为
的衍生抛物线为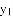 ,其顶点为
,其顶点为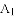 ;关于点
;关于点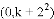 的衍生抛物线为
的衍生抛物线为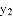 ,其顶点为
,其顶点为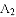 ;…;关于点
;…;关于点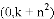 的衍生抛物线为
的衍生抛物线为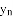 ,其顶点为
,其顶点为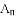 ;…(
;…(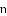
正整数).求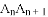 的长(用含
的长(用含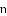

查看答案和解析>>
科目:初中数学 来源:江西省等学校招生考试数学试卷 题型:解答题
今年某市为创评“全国文明城市”称号,周末团市委组织志愿者进行宣传活动.班主任梁老师决定从4名女班干部(小悦、小惠、小艳和小倩)中通过抽签的方式确定2名女生去参加.
抽签规则:将4名女班干部姓名分别写在4张完全相同的卡片正面,把四张卡片背面朝上,洗匀后放在桌面上,梁老师先从中随机抽取一张卡片,记下姓名,再从剩余的3张卡片中随机抽取第二张,记下姓名.
(1)该班男生“小刚被抽中”是 事件,“小悦被抽中”是 事件(填“不可能”或“必然”或“随机”);第一次抽取卡片“小悦被抽中”的概率为 ;
(2)试用画树状图或列表的方法表示这次抽签所有可能的结果,并求出“小惠被抽中”的概率.
查看答案和解析>>
科目:初中数学 来源:2018年嘉兴市毕业生学业考试适应性练习(二)数学试卷卷 题型:解答题
我们把有两条边和其中一边的对角对应相等的两个三角形叫做友好三角形。如图,在△ABC和△ABD中,AB=AB,AD=AC,∠ABC=∠ABD,则△ABC和△ABD是友好三角形。
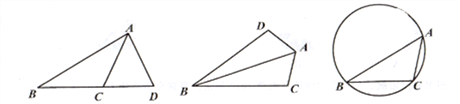
(1)如图1,已知AD=AC,请写出图中的友好三角形;
(2)如图2,在△ABC和△ABD中,AD=AC,∠BDA=∠BCA,且∠BDA>90°,
求证:△ABC≌△ABD;
(3) 如图3,△ABC内接于圆,∠ABC=30°,∠BAC=45°,BC=4。D是圆上一点,若△ABD和△ABC是友好三角形,且BD<AD,求AD的长。
查看答案和解析>>
科目:初中数学 来源:湖南省邵阳市大祥区2018年中考数学考前押题卷 题型:单选题
如图,把菱形ABCD沿AH折叠,使B点落在BC上的E点处,若∠B=70°,则∠EDC的大小为( )
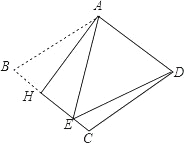
A. 10° B. 15° C. 20° D. 30°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com