
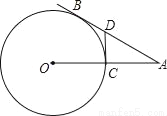
��ͼ��AB�С�O�ڵ�B��OA����O��C�㣬��C��DC��OA��AB��D����BD��AD=1��2��
��1�����A������ֵ��
��2����OC=1����AB��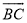 �ij���
�ij���

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ���㽭ʡ������2018����꼶�ϲ���ĩģ����ѧ�Ծ� ���ͣ������
��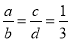 ��b+d��0������
��b+d��0������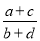 =________
=________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017������ʡӪ���д�ʯ����ˮԴ���п���ѧģ���Ծ������� ���ͣ���ѡ��
��1.5�ľ���ֵ�ǣ�������
A. 0 B. ��1.5 C. 1.5 D. 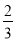
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ��������ɽ�羰��2017-2018ѧ����꼶����ĩģ����ѧ�Ծ� ���ͣ���ѡ��
ֱ��L��һ���ӣ�P��Q��������ׯ������L�ϵ�ij����һ��ˮ��վ����P��Q���ع�ˮ�����������������跽����ͼ��ʵ�߱�ʾ����Ĺܵ���������ܵ���̵��ǣ���������
A. 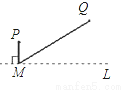 B.
B. 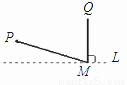
C. 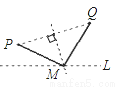 D.
D. 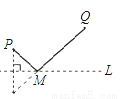
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ��������ɽ�羰��2017-2018ѧ����꼶����ĩģ����ѧ�Ծ� ���ͣ������
��ABC�У�DF��AB�Ĵ�ֱƽ���ߣ���BC��D��EG��AC�Ĵ�ֱƽ���ߣ���BC��E������DAE=30�㣬���BAC����________��
75�㣮 �������������������ͼ�� ��DF��AB�Ĵ�ֱƽ���ߣ�EG��AC�Ĵ�ֱƽ���ߣ� ��DA=DB��EC=EA�� ���B=��BAD����C=��CAE�� �ߡ�DAE=��BAD+��CAE����BAC���ҡ�DAE=30�㣬 ��30��=��B+��C����BAC����30��=��180�㩁��BAC������BAC�� ��á�BAC=75�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ʡ�˲����п���ѧģ���Ծ������� ���ͣ������
��ͼ����ƽ���ı���ABCD�У���ABC�͡�ADC��ƽ���߷ֱԱ��ڵ�E��F�����ı��εĶԽ���AC�ڵ�G��H����֤��AH=CG��
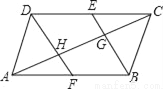
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ʡ�˲����п���ѧģ���Ծ������� ���ͣ���ѡ��
�����ĸ�������
��y=kx��k������k��0��
��y=kx+b��k��b������k��0��
��y=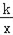 ��k������k��0��x��0��
��k������k��0��x��0��
��y=ax2��a������a��0��
���У�����y��ֵ����xֵ����������ٵ��ǣ�������
A. �� B. �� C. �� D. ��
C �������������������y=kx��kΪ������k��0������������������y����x����������� ��y=kx+b��k��bΪ������k��0����һ�κ�������y����x����������� ��y=��kΪ������k��0������������������ÿ�������y��x���������С����ȷ�� ��y=ax2��aΪ������a��0����ͼ���ڶԳ����Ҳ࣬y����x������������ڶԳ�����࣬y����x���������С������...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭ʡ����2018����꼶�ϲ���ĩģ����ѧ�Ծ� ���ͣ������
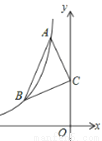
��ͼ����֪��A��B�Ƿ���������y=��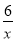 ���ڵڶ������ڵķ�֧�ϵ������㣬��C��0��3�����ҡ�ABC����AC=BC����ACB=90�㣬���߶�AB�ij�Ϊ__��
���ڵڶ������ڵķ�֧�ϵ������㣬��C��0��3�����ҡ�ABC����AC=BC����ACB=90�㣬���߶�AB�ij�Ϊ__��
���𰸡�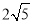
������������A��AD��y���ڵ�D������B��BE��y���ڵ�E������A��AF��BE���ڵ�F����ͼ��ʾ��
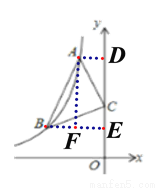
�ߡ�ACB=90�㣬
���ACD+��BCE=90�㣬
�֡�AD��y�ᣬBE��y�ᣬ
���ACD+��CAD=90�㣬��BCE+��CBE=90�㣬
���ACD=��CBE����BCE=��CAD��
�ڡ�ACD�͡�CBE�У���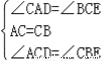 ��
��
���ACD�ա�CBE��ASA����
���B��������m���� ����m��0������E��0����
����m��0������E��0���� ������D��0��3��m������A����
������D��0��3��m������A���� ��3��3��m����
��3��3��m����
�ߵ�A���� ��3��3��m���ڷ���������y=��
��3��3��m���ڷ���������y=�� �ϣ�
�ϣ�
 ����ã�m=��3��m=2����ȥ����
����ã�m=��3��m=2����ȥ����
���A����������1��6������B����������3��2������F����������1��2����
��BF=2��AF=4��
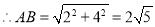
�ʴ�Ϊ��2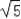 ��
��
���㾦��
����A��AD��y���ڵ�D������B��BE��y���ڵ�E������A��AF��BE���ڵ�F,���ݽǵļ���ó�����ACD=��CBE����BCE=��CAD�����ɴ�֤����ACD�ա�CBE�������B������Ϊ��m���� ������������ȫ���ҳ���A�����꣬����A��������뵽��������������ʽ�����m��ֵ����m��ֵ����A��B�����꼴�ɵó���A��B�����꣬����ϵ�A��B�����������F�����꣬���ù��ɶ������ɵó����ۣ�
������������ȫ���ҳ���A�����꣬����A��������뵽��������������ʽ�����m��ֵ����m��ֵ����A��B�����꼴�ɵó���A��B�����꣬����ϵ�A��B�����������F�����꣬���ù��ɶ������ɵó����ۣ�
�����͡������
��������
18
���κ���y=x2+��2m+1��x+��m2��1������Сֵ��2����m=________��
������������������߶��κ�������Сֵ��2�� ��y=���� ��ã�m=.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017��ӱ�ʡ�п���ѧģ���Ծ� ���ͣ���ѡ��
A��B�������180km�����ĸ��ٹ�·��ͨ����A��B���ؼ���ʻ�ij�;�ͳ�ƽ�����������50%������A�ص�B�ص�ʱ��������1h������ԭ����ƽ������Ϊxkm/h�������������з���Ϊ
A. 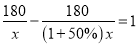 B.
B. 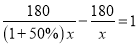
C. 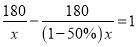 D.
D. 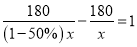
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com