
直线L是一条河,P,Q是两个村庄.欲在L上的某处修建一个水泵站,向P,Q两地供水,现有如下四种铺设方案,图中实线表示铺设的管道,则所需管道最短的是( ).
A. 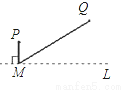 B.
B. 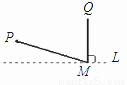
C. 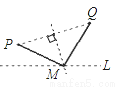 D.
D. 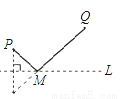
科目:初中数学 来源:浙江杭州拱墅区文澜中学2018届九年级上学期期中考试数学试卷(含解析) 题型:单选题
如图,点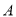 、
、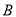 、
、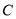 在⊙
在⊙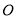 上,
上, 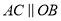 ,
, 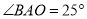 ,则
,则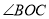 的度数为( ).
的度数为( ).

A.  B.
B. 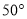 C.
C. 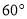 D.
D. 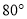
查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(二) 题型:填空题
分解因式:m4n﹣4m2n=_____.
m2n(m+2)(m﹣2) 【解析】原式=m2n(m2﹣4)=m2n(m+2)(m﹣2), 故答案为:m2n(m+2)(m﹣2)查看答案和解析>>
科目:初中数学 来源:山东省临朐县沂山风景区2017-2018学年八年级上期末模拟数学试卷 题型:解答题
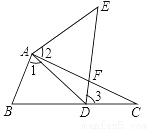
如图,点E在△ABC外部,点D在BC边上,DE交AC于点F,若∠1=∠2=∠3,AC=AE,求证:AB=AD.
查看答案和解析>>
科目:初中数学 来源:山东省临朐县沂山风景区2017-2018学年八年级上期末模拟数学试卷 题型:单选题
如图,在Rt△ABC中,∠A=90°,∠ABC的平分线BD交AC于点D,AD=3,BC=10,则△BDC的面积是( )
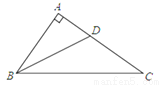
A. 10 B. 15 C. 20 D. 30
B 【解析】【解析】 过D作DE⊥BC于E. ∵∠A=90°,∴DA⊥AB.∵BD平分∠ABC,∴AD=DE=3,∴△BDC的面积是×DE×BC=×10×3=15,故选B.查看答案和解析>>
科目:初中数学 来源:山东省临朐县沂山风景区2017-2018学年八年级上期末模拟数学试卷 题型:填空题
用反证法证明“一个三角形中至多有一个钝角”时,应假设 .
一个三角形中至少有两个钝角. 【解析】 试题分析:用反证法证明的第一步就是作出与原命题相矛盾的假设,因此用反证法证明“一个三角形中至多有一个钝角”时,第一步应假设一个三角形中至少有两个钝角.查看答案和解析>>
科目:初中数学 来源:2017年湖北省宜昌市中考数学模拟试卷(三) 题型:解答题
如图,AB切⊙O于点B,OA交⊙O于C点,过C作DC⊥OA交AB于D,且BD:AD=1:2.
(1)求∠A的正切值;
(2)若OC=1,求AB及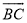 的长.
的长.
查看答案和解析>>
科目:初中数学 来源:2017年湖北省宜昌市中考数学模拟试卷(三) 题型:单选题
一只小鸟自由自在地在空中飞行,然后随意落在图中所示的某个方格中(每个方格除颜色外完全一样),那么小鸟停在黑色方格中的概率是( )

A. 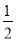 B.
B. 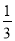 C.
C. 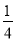 D.
D. 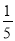
查看答案和解析>>
科目:初中数学 来源:2017年河北省中考数学模拟试卷 题型:单选题
已知抛物线y=x2-(2m+1)x+2m不经过第三象限,且当x>2时,函数值y随x的增大而增大,则实数m的取值范围是( )
A. 0≤m≤1.5 B. m≥1.5 C. 0≤m≤1 D. 0<m≤1.5
A 【解析】根据当x>2时,抛物线y=x2﹣(2m+1)x+2m满足y随x的增大而增大,可由抛物线的对称轴,得≤2,解得m≤1.5.然后根据抛物线开口向上,且不经过第三象限,得到2m≥0,解得,m≥0,因此可得m的取值范围为:0≤m≤1.5, 故选:A.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com