
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:北京市2017-2018学年第一学期八年级数学期中试卷 题型:填空题
多项式x2﹣8x+k是一个完全平方式,则k=_____.
16 【解析】k=(-4)2=16. 故答案为16.查看答案和解析>>
科目:初中数学 来源:福建省2016-2017学年八年级下学期期末考试数学试卷 题型:解答题
在一条笔直的公路上有 、
、 两地,甲从
两地,甲从 地去
地去 地,乙从
地,乙从 地去
地去 地然后立即原路返回
地然后立即原路返回 地,返回时的速度是原来的2倍,如图是甲、乙两人离
地,返回时的速度是原来的2倍,如图是甲、乙两人离 地的距离
地的距离 (千米)和时间
(千米)和时间 (小时)之间的函数图象.
(小时)之间的函数图象.

请根据图象回答下列问题:
(1) 、
、 两地的距离是 千米,
两地的距离是 千米,  ;
;
(2)求 的坐标,并解释它的实际意义;
的坐标,并解释它的实际意义;
(3)请直接写出当 取何值时,甲乙两人相距15千米.
取何值时,甲乙两人相距15千米.
查看答案和解析>>
科目:初中数学 来源:福建省2016-2017学年八年级下学期期末考试数学试卷 题型:单选题
下列命题正确的是( )
A. 对角线互相平分的四边形是平行四边形
B. 对角线互相垂直的四边形是菱形
C. 对角线相等的四边形是矩形
D. 对角线互相垂直且相等的四边形是正方形
A 【解析】A. 对角线互相平分的四边形是平行四边形,说法正确; B. 对角线互相垂直的四边形是菱形,说法错误,应为对角线互相垂直且平分的四边形是菱形; C. 对角线相等的四边形是矩形,说法错误,应为对角线相等且平分的四边形是矩形; D. 对角线互相垂直且相等的四边形是正方形,说法错误,应为对角线互相垂直且相等的平行四边形是正方形; 故选:A.查看答案和解析>>
科目:初中数学 来源:上海市黄浦区2018届九年级上学期期末调研测试数学试卷(WORD版) 题型:解答题
在平面直角坐标系xOy中,对称轴为直线x=1的抛物线y=ax2+bx+8过点(﹣2,0).
(1)求抛物线的表达式,并写出其顶点坐标;
(2)现将此抛物线沿y轴方向平移若干个单位,所得抛物线的顶点为D,与y轴的交点为B,与x轴负半轴交于点A,过B作x轴的平行线交所得抛物线于点C,若AC∥BD,试求平移后所得抛物线的表达式.
查看答案和解析>>
科目:初中数学 来源:上海市黄浦区2018届九年级上学期期末调研测试数学试卷(WORD版) 题型:填空题
已知抛物线y=ax2+bx+c开口向上,一条平行于x轴的直线截此抛物线于M、N两点,那么线段MN的长度随直线向上平移而变_____.(填“大”或“小”)
大 【解析】因为二次函数的开口向上,所以点M,N向上平移时,距离对称轴的距离越大,即MN的长度随直线向上平移而变大,故答案为:大.查看答案和解析>>
科目:初中数学 来源:上海市黄浦区2018届九年级上学期期末调研测试数学试卷(WORD版) 题型:填空题
已知a、b、c满足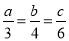 ,a、b、c都不为0,则
,a、b、c都不为0,则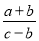 =_____.
=_____.
查看答案和解析>>
科目:初中数学 来源:北京市西城外国语学校2017-2018学年度第一学期八年级数学期中试卷 题型:解答题
把下列各式因式分解
(1)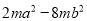 (2)
(2) 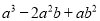 (3)
(3) 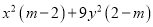
查看答案和解析>>
科目:初中数学 来源:黑龙江省大庆市2016---2017学年度上期初三数学期末试卷 题型:单选题
一次智力测验,有20道选择题.评分标准是:对1题给5分,错1题扣2分,不答题不给分也不扣分.小明有两道题未答.至少答对几道题,总分才不会低于60分.则小明至少答对的题数是( )
A.11道 B。12题 C.13题 D.14题
D 【解析】设小明至少答对的题数是x道, 5x-2(20-2-x)≥60, x≥135/7 , 故应为14. 故选D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com