
2012年5月,在中国武汉举办了汤姆斯杯羽毛球团体赛.在27日的决赛中,中国队战胜韩国队夺得了冠军.某羽毛球协会组织一些会员到现场观看了该场比赛.已知该协会购买了每张300元和每张400元的两种门票共8张,总费用为2700元.请问该协会购买了这两种门票各多少张?
每张300元的门票买了5张,每张400元的门票买了3张. 【解析】试题分析:设每张300元的门票买了x张,则每张400元的门票买了(8-x)张,根据题意建立方程,求出方程的解就可以得出结论. 试题解析:设每张300元的门票买了x张,则每张400元的门票买了(8-x)张, 由题意,得300x+400(8-x)=2700, 解得:x=5, 所以买400元每张的门票张数为:... 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:初中数学 来源:安徽省巢湖市2016~17学年度第一学期 期末教学质量检测 八年级数学试卷 题型:解答题
已知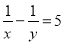 ,求
,求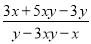 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:湖南省2017-2018学年七年级数学上期末复习检测数学试卷 题型:单选题
下列五个算式,①a4·a3=a12;②a3+a5=a8;③a5÷a5=a;④(a3)3=a6;⑤a5+a5=2a5,其中正确的个数有( )
A. 0个 B. 1个 C. 2个 D. 3个
B 【解析】∵①a4•a3=a7;②a3与a5不能合并;③a5÷a5=1;④(a3)3=a9;⑤a5+a5=2a5 , ∴①②③④错误,⑤正确, 故选B.查看答案和解析>>
科目:初中数学 来源:黑龙江省2017-2018学年七年级数学上学期期末试卷 题型:填空题
下列说法正确的是( )
A. 3不是单项式 B. 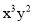 没有系数
没有系数
C. 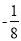 是一次一项式 D.
是一次一项式 D. 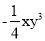 是单项式
是单项式
查看答案和解析>>
科目:初中数学 来源:黑龙江省2017-2018学年七年级数学上学期期末试卷 题型:单选题
有理数m,n在数轴上的位置如图所示,则化简│n│-│m-n│的结果是( )
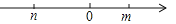
A. m B. 2n-m C. -m D. m-2n
C 【解析】根据数轴的特点,可知n<0<m,且|n|>|m|,因此可知m-n>0,所以根据绝对值的意义可知│n│-│m-n│=-n-m+n=-m. 故选:C.查看答案和解析>>
科目:初中数学 来源:宁夏2017-2018学年第一学期七年级上册数学期末试卷 题型:填空题
某市在端午节准备举行划龙舟大赛,预计15个队共330人参加.已知每个队一条船,每条船上人数相等,且每条船上有1人击鼓,1人掌舵,其余的人同时划桨.设每条船上划桨的有x人,那么可列出一元一次方程为__.
15(x+2)=330 【解析】设每条船上划桨的有x人,则每条船上有(x+2)人,根据等量关系列方程得:15(x+2)=330. 故答案为:15(x+2)=330.查看答案和解析>>
科目:初中数学 来源:宁夏2017-2018学年第一学期七年级上册数学期末试卷 题型:单选题
如图所示,已知∠AOC=∠BOD=80°,∠BOC=30°,则∠AOD的度数为( )
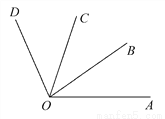
A. 160° B. 110° C. 130° D. 140°
C 【解析】因为∠AOC=80°,∠BOC=30°, 所以∠AOB=∠AOC-∠BOC=80°-30°=50°, 又因为∠BOD=80°, 所以∠AOD=∠AOB+∠BOD=50°+80°=130°. 故选:C.查看答案和解析>>
科目:初中数学 来源:2017-2018学年度第一学期海南省海口市九年级数学科期末检测题 题型:单选题
如图,平面直角坐标系内有一点P(3,4),连接OP,则cos α等于( )
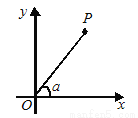
A. 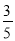 B.
B. 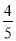 C.
C. 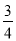 D.
D. 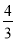
查看答案和解析>>
科目:初中数学 来源:湖北省襄阳市襄城区2016-2017学年度上学期期末考试九年级数学试卷 题型:解答题
如图,CD是⊙O的直径,AB是⊙O的弦,AB⊥CD于G,OG:OC=3:5,AB=8.
(1)求⊙O的半径;
(2)点E为圆上一点,∠ECD=15º,将弧CE沿弦CE翻折,交CD于点F,求图中阴影部分的面积.
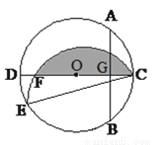
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com