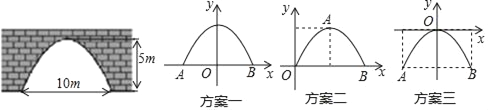
如图，是一座古拱桥的截面图，拱桥桥洞的上沿是抛物线形状，当水面的宽度为10m时，桥洞与水面的最大距离是5m．
（1）经过讨论，同学们得出三种建立平面直角坐标系的方案（如图），你选择的方案是 （填方案一，方案二，或方案三），则B点坐标是 ，求出你所选方案中的抛物线的表达式；
（2）因为上游水库泄洪，水面宽度变为6m，求水面上涨的高度．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：初中数学 来源：河南省2018届九年级中考数学二模试卷（A卷） 题型：解答题
因商人、商业、商品发源于商丘，商朝建都于河南商丘，商丘被誉为“三商之源，华商之都”
，小亮在写字楼前F处，测得商字雕塑的顶端A的仰角为
，有装B，F，D在同一条直线上，
，
，
．
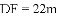
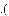
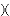
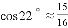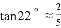查看答案和解析>>
科目：初中数学 来源：山西省吕梁市柳林县2017-2018学年七年级下学期期末考试数学试卷 题型：解答题
已知如图，直线EF与AB、CD分别相交于点E、F．
（1）如图1，若∠1=120°，∠2=60°，求证AB∥CD；
（2）在（1）的情况下，若点P是平面内的一个动点，连结PE、PF，探索∠EPF、∠PEB、∠PFD三个角之间的关系；
①当点P在图2的位置时，可得∠EPF=∠PEB+∠PFD；
请阅读下面的解答过程，并填空（理由或数学式）
【解析】
如图2，过点P作MN∥AB，
则∠EPM=∠PEB_____．
∵AB∥CD（已知），MN∥AB（作图）
∴MN∥CD_____．
∴∠MPF=∠PFD
∴∠_____+∠_____=∠PEB+∠PFD（等式的性质）
即∠EPF=∠PEB+∠PFD
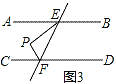
②当点P在图3的位置时，∠EPF、∠PEB、∠PFD三个角之间有何关系并证明．
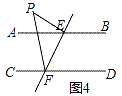
③当点P在图4的位置时，请直接写出∠EPF、∠PEB、∠PFD三个角之间的关系：_____．
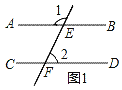
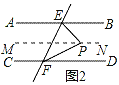
查看答案和解析>>
科目：初中数学 来源：山西省吕梁市柳林县2017-2018学年七年级下学期期末考试数学试卷 题型：单选题
为了了解全校七年级300名学生的视力情况，骆老师从中抽查了50名学生的视力情况．针对这个问题，下面说法正确的是（ ）
A. 300名学生是总体 B. 每名学生是个体
C. 50名学生是所抽取的一个样本 D. 这个样本容量是50
查看答案和解析>>
科目：初中数学 来源：北京市昌平区2017-2018学年九年级上学期期末考试试卷 题型：解答题
对于平面直角坐标系xOy中的点P，给出如下定义：记点P到x轴的距离为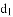
，到y轴的距离为
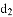，若
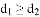，则称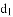为点P的最大距离；若
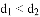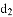，则称为点P的最大距离.
例如：点P（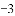
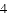
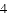
（1）①点A（2，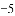
②若点B（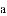
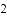
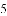
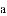
（2）若点C在直线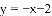
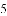
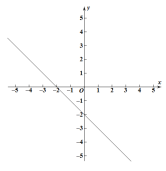
（3）若⊙O上存在点M，使点M的最大距离为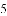
查看答案和解析>>
科目：初中数学 来源：北京市昌平区2017-2018学年九年级上学期期末考试试卷 题型：解答题
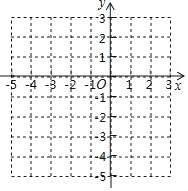
二次函数图象上部分点的横坐标x，纵坐标y的对应值如下表：
x | … | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 5 | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | 5 | … |
（1）求这个二次函数的表达式；
（2）在图中画出这个二次函数的图象．
查看答案和解析>>
科目：初中数学 来源：北京市昌平区2017-2018学年九年级上学期期末考试试卷 题型：填空题
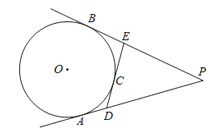
如图，PA，PB分别与⊙O相切于A、B两点，点C为劣弧AB上任意一点，过点C的切线分别交AP，BP于D，E两点．若AP=8，则△PDE的周长为__________．
查看答案和解析>>
科目：初中数学 来源：吉林省长春市2018届九年级中考二模数学试卷 题型：填空题
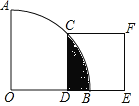
如图，在扇形AOB中，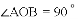
，
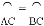，过点C作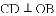
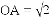，则阴影部分的面积是______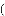
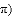
查看答案和解析>>
科目：初中数学 来源：广东省潮州市湘桥区2017-2018学年八年级下学期期末考试数学试卷 题型：填空题
某公司招聘一名人员，应聘者小王参加面试和笔试，成绩（100分制）如表所示：
面试 | 笔试 | |||
成绩 | 评委1 | 评委2 | 评委3 | 92 |
88 | 90 | 86 |
如果面试平均成绩与笔试成绩按6：4的比确定，请计算出小王的最终成绩_____．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
