
如图,在宽为20米,长为32米的矩形地面上修筑同样宽的道路(图中阴影部分),余下部分种植草坪,要使草坪的面积为540平方米,设道路的宽为x米,则下列方程正确的是( )
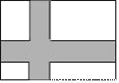
A. 32×20﹣20x﹣30x=540 B. 32×20﹣20x﹣30x﹣x2=540
C. (32﹣x)(20﹣x)=540 D. 32×20﹣20x﹣30x+2x2=540
C 【解析】 如图,将小路平移,则草地的长为(32-x)米,小路的宽为(20-x)米,故可列方程为: (32﹣x)(20﹣x)=540 . 故选C.科目:初中数学 来源:内蒙古2017-2018学年七年级上学期期末考试数学试卷 题型:解答题
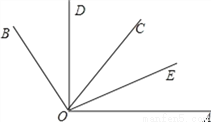
如图,OD平分∠BOC,OE平分∠AOC.若∠BOC=70°,∠AOC=50°.
(1)求出∠AOB及其补角的度数;
(2)请求出∠DOC和∠AOE的度数,并判断∠DOE与∠AOB是否互补,并说明理由.
查看答案和解析>>
科目:初中数学 来源:江苏省南通市2017-2018学年七年级上学期第三次月考数学试卷 题型:填空题
三个连续奇数的和是75,这三个数分别是__________.
23,25,27 【解析】设中间奇数为x,则前一个为x-2,后一个为x+3,由题意得 x-2+x+x+2=75,解之得x=25, ∴x-2=23,x+2=27. ∴这三个数分别是23,25,27,.查看答案和解析>>
科目:初中数学 来源:云南省2018届九年级上学期期末考试数学试卷 题型:解答题
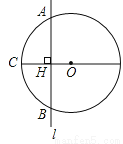
如图,⊙O的半径OC=10cm,直线l⊥CO,垂足为H,交⊙O于A,B两点,AB=16cm,直线l平移多少厘米时能与⊙O相切
查看答案和解析>>
科目:初中数学 来源:云南省2018届九年级上学期期末考试数学试卷 题型:填空题
若点(a,1)与(-2,b)关于原点对称,则ab=________.
【解析】试题分析:平面直角坐标系中任意一点P(x,y),关于原点的对称点是(﹣x,﹣y),即:求关于原点的对称点,横纵坐标都变成相反数.记忆方法是结合平面直角坐标系的图形记忆. 【解析】 ∵点(a,1)与(﹣2,b)关于原点对称, ∴b=﹣1,a=2, ∴ab=2﹣1=. 故答案为:.查看答案和解析>>
科目:初中数学 来源:四川外语学院重庆第二外国语学校2018届九年级上学期第二次月考数学试卷 题型:解答题
如图,在平面直角坐标系中,抛物线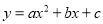 与x轴交于B(-3,0)、C(1,0)两点,与y轴交于点A(0,2),抛物线的顶点为D.连接AB,点E是第二象限内的抛物线上的一动点,过点E作EP⊥BC于点P,交线段AB于点F.
与x轴交于B(-3,0)、C(1,0)两点,与y轴交于点A(0,2),抛物线的顶点为D.连接AB,点E是第二象限内的抛物线上的一动点,过点E作EP⊥BC于点P,交线段AB于点F.
(1)求此抛物线的解析式;
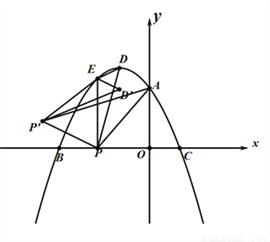
(2)过点E作EG⊥AB于点G,Q为线段AC的中点,当△EGF周长最大时,在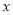 轴上找一点R,使得|RE-RQ|值最大,请求出R点的坐标及|RE-RQ|的最大值;
轴上找一点R,使得|RE-RQ|值最大,请求出R点的坐标及|RE-RQ|的最大值;
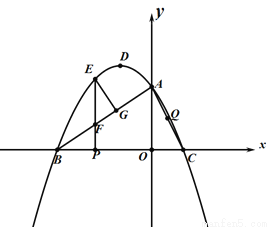
(3)在(2)的条件下,将△PED绕E点旋转得△ED′P′,当△AP′P是以AP为直角边的直角三角形时,求点P′的坐标.
查看答案和解析>>
科目:初中数学 来源:四川外语学院重庆第二外国语学校2018届九年级上学期第二次月考数学试卷 题型:解答题
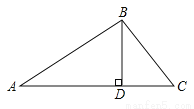
如图,在△ABC中,BD⊥AC,AB=8,AC=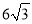 ,∠A=30°.
,∠A=30°.
(1)请求出线段AD的长度;
(2)请求出sin∠C的值.
查看答案和解析>>
科目:初中数学 来源:四川外语学院重庆第二外国语学校2018届九年级上学期第二次月考数学试卷 题型:单选题
如图所示的几何体的俯视图是( )
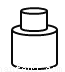
A. 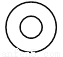 B.
B. 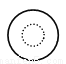 C.
C. 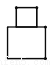 D.
D. 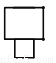
查看答案和解析>>
科目:初中数学 来源:江苏省盐城市盐都区2016-2017学年八年级上学期期末联考数学试卷 题型:填空题
比较大小: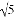 __2(填“>”或“<”或“=”)
__2(填“>”或“<”或“=”)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com