
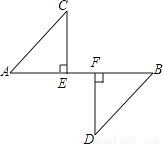
如图,CE⊥AB,DF⊥AB,垂足分别为E、F,AC∥DB,且AC=BD,那么Rt△AEC≌Rt△BFC的理由是( )
A.SSS B.AAS C.SAS D.HL
B 【解析】【解析】 ∵CE⊥AB,DF⊥AB, ∴∠AEC=∠BFD=90°. ∵AC∥DB, ∴∠A=∠B. 在△AEC和△BFD中 , ∴Rt△AEC≌Rt△BFC(AAS), 故选B.科目:初中数学 来源:山东省2018届九年级上期末模拟数学试卷(解析版) 题型:解答题
图①为一种平板电脑保护套的支架效果图,AM固定于平板电脑背面,与可活动的MB、CB部分组成支架.平板电脑的下端N保持在保护套CB上.不考虑拐角处的弧度及平板电脑和保护套的厚度,绘制成图②.其中AN表示平板电脑,M为AN上的定点,AN=CB=20 cm,AM=8 cm,MB=MN.我们把∠ANB叫做倾斜角.
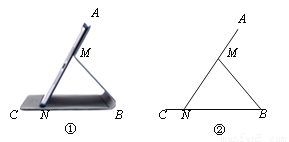
(1)当倾斜角为45°时,求CN的长;
(2)按设计要求,倾斜角能小于30°吗?请说明理由.
(1) (20-12)cm.(2)不能,理由见解析. 【解析】 试题分析:(1)当∠ANB=45°时,根据等腰三角形的性质可得∠NMB=90°.再根据等腰直角三角形的性质和三角函数可得BN的长度,根据CN=CB-BN=AN-BN即可求解; (2)当∠ANB=30°时,作ME⊥CB,垂足为E.根据三角函数可得BN=2BE=12cm,CB=AN=20cm,依此即可作出判断. 试...查看答案和解析>>
科目:初中数学 来源:甘肃省酒泉市2017-2018学年第一学期七年级数学试卷 题型:单选题
点A点B点C在一条直线上,已知线段AB=10cm,BC=3cm,则线段AC的长是( )
A. 13cm B. 7cm C. 13cm或7cm D. 以上答案都不对
C 【解析】当点C在线段AB上,如图1,则AC=AB?BC=10cm?3cm=7cm; 当点C在线段AB的延长线上,如图2,则AC=AB+BC=10cm+3cm=13cm, 所以A.C两点之间的距离为7cm或13cm. 故选C.查看答案和解析>>
科目:初中数学 来源:2017-2018学年山东省诸城市 八年级上期末模拟数学试卷 题型:填空题
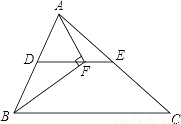
如图,在△ABC中BF平分∠ABC,AF⊥BF于点F,D为AB的中点,连接DF延长交AC于点E.若AB=12,BC=16,则线段EF的长为________.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年山东省诸城市 八年级上期末模拟数学试卷 题型:单选题
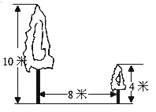
如图,有两棵树,一棵高10米,另一棵高4米,两树相距8米,一只小鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行( )
A. 8米 B. 10米 C. 12米 D. 14米
B 【解析】试题分析:连接两棵树的顶点,然后利用勾股定理可得:小鸟飞行的长度==10米.查看答案和解析>>
科目:初中数学 来源:山东省枣庄市滕州市2017-2018学年八年级(上)期中数学试卷 题型:解答题
“珍重生命,注意安全!”同学们在上下学途中一定要注意骑车安全.小明骑单车上学,当他骑了一段时,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校,以下是他本次所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:
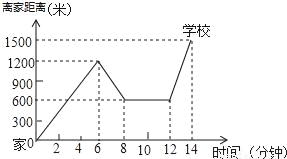
(1)小明家到学校的路程是多少米?
(2)小明在书店停留了多少分钟?
(3)本次上学途中,小明一共行驶了多少米?一共用了多少分钟?
(4)我们认为骑单车的速度超过300米/分钟就超越了安全限度.问:在整个上学的途中哪个时间段小明骑车速度最快,速度在安全限度内吗?
(1)1500米;(2)4分钟;(3)2700米,14分钟;(4)12~14分钟时速度最快,不在安全限度内 【解析】试题分析:(1)根据函数图象的纵坐标,可得答案; (2)根据函数图象的横坐标,可得到达书店时间,离开书店时间,根据有理数的减法,克的答案; (3)根据函数图象的纵坐标,可得相应的路程,根据有理数的加法,可得答案; (4)根据函数图象的纵坐标,可得路程,根据函数...查看答案和解析>>
科目:初中数学 来源:山东省枣庄市滕州市2017-2018学年八年级(上)期中数学试卷 题型:填空题
如图,长方体的底面边长分别为1cm 和3cm,高为6cm.如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需要_____cm.
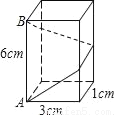
查看答案和解析>>
科目:初中数学 来源:山东省枣庄市滕州市2017-2018学年八年级(上)期中数学试卷 题型:单选题
若点A(2,m)在x轴上,则点B(m-1,m+1)在 ( D )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
D 【解析】【解析】 ∵点A(2,m)在x轴上, ∴m=0, ∴点B(m+1,m﹣1)为(1,﹣1),在第四象限. 故选D.查看答案和解析>>
科目:初中数学 来源:江苏省无锡市2018届九年级12月月考数学试卷 题型:填空题
如图,AB为⊙O的直径,弦CD⊥AB于E,已知CD=12,AB=20.则OE=_______.
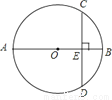
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com