练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

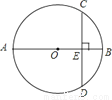
    如图，AB为⊙O的直径，弦CD⊥AB于E，已知CD=12，AB=20．则OE=_______.

    8 【解析】试题分析：∵直径AB＝20， ∴半径为10， 连接OC， ∵AB为⊙O的直径，弦CD⊥AB于E，CD＝12， ∴CE＝DE＝6， 由勾股定理得：OC2＝CE2＋OE2， 102＝62＋OE2， ∴OE＝8， 故答案为8．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017-2018学年山东省诸城市 八年级上期末模拟数学试卷 题型：单选题

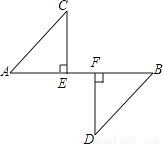
    如图，CE⊥AB，DF⊥AB，垂足分别为E、F，AC∥DB，且AC=BD，那么Rt△AEC≌Rt△BFC的理由是（ ）

    A．SSS B．AAS C．SAS D．HL

    B 【解析】【解析】 ∵CE⊥AB，DF⊥AB， ∴∠AEC=∠BFD=90°． ∵AC∥DB， ∴∠A=∠B． 在△AEC和△BFD中 ， ∴Rt△AEC≌Rt△BFC（AAS）， 故选B．

    查看答案和解析>>

    科目：初中数学 来源：北师大版数学八年级上册期末测评 题型：填空题

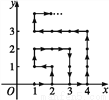
    如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2),(2,2),….根据这个规律,第2 025个点的坐标为________.

    (45,0) 【解析】试题解析：观察图形可知，到每一横坐标结束，经过整数点的点的总个数等于最后点的横坐标的平方，并且横坐标是奇数时最后以横坐标为该数，纵坐标为0结束，当横坐标是偶数时，以横坐标为1，纵坐标为横坐标减1的点结束，根据此规律解答即可： 横坐标为1的点结束，共有1个，1=12， 横坐标为2的点结束，共有2个，4=22， 横坐标为3的点结束，共有9个，9=32， ...

    查看答案和解析>>

    科目：初中数学 来源：江苏省无锡市2018届九年级12月月考数学试卷 题型：解答题

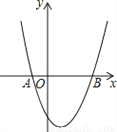
    如图，已知抛物线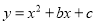经过A（﹣1，0）、B（3，0）两点．

    （1）求抛物线的解析式和顶点坐标；

    （2）当0＜x＜3时，求y的取值范围；

    （3）点P为抛物线上一点，若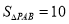，求出此时点P的坐标．

    （1）抛物线的解析式为y=x2﹣2x﹣3，顶点坐标为（1，﹣4）；（2）由图可得当0＜x＜3时，﹣4≤y＜0；（3）P点坐标为（﹣2，5）或（4，5）． 【解析】试题分析：（1）由点A、B的坐标利用待定系数法即可求出抛物线的解析式，再利用配方法即可求出抛物线顶点坐标； （2）结合函数图象以及A、B点的坐标即可得出结论； （3）设P（x，y），根据三角形的面积公式以及S△PAB＝1...

    查看答案和解析>>

    科目：初中数学 来源：江苏省无锡市2018届九年级12月月考数学试卷 题型：解答题

    计算：（1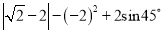）； （2）

    （1）-2；（2）4. 【解析】试题分析：（1）先化简绝对值，计算乘方，代入特殊角的三角函数值计算，然后合并同类二次根式即可； （1）先计算算术平方根，负指数幂，代入特殊角的三角函数值，计算0次幂，最后相加减即可． 试题解析： 【解析】 （1）原式＝＝－2； （2）原式＝2＋2－2×＋1＝4－1＋1＝4.

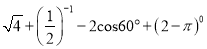
    查看答案和解析>>

    科目：初中数学 来源：江苏省无锡市2018届九年级12月月考数学试卷 题型：单选题

    如图所示，直线CD与线段AB为直径的圆相切于点D，并交BA的延长线于点C，且AB=2，AD=1，P点在切线CD上移动．当∠APB的度数最大时，则∠ABP的度数为（ ）

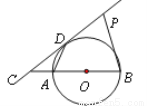
    A. 90° B. 60° C. 45° D. 30°

    D 【解析】试题分析：连接BD, ∵直线CD与以线段AB为直径的圆相切于点D, ∴∠ADB=90°, 当∠APB的度数最大时, 则P和D重合, ∴∠APB=90°, ∵AB=2,AD=1, ∴sin∠ABP=, ∴∠ABP=30°, ∴当∠APB的度数最大时,∠ABP的度数为30°． 故选：D．

    查看答案和解析>>

    科目：初中数学 来源：江苏省无锡市2018届九年级12月月考数学试卷 题型：单选题

    在Rt△ABC中，∠C＝90°，∠B＝35°，AB＝7，则BC的长为（ ）

    A. 7sin35° B. 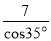C. 7cos35° D. 7tan35°

    C 【解析】试题分析：由cosB＝， 得BC＝ABcosB＝7cos35°， 故选C．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年第一学期期末复习备考之精准复习模拟题七年级浙教版数学试卷（C卷） 题型：单选题

    如图，M，N为线段AB的三等分点，P为MN的中点，则下列结论：①M为AN的中点，N为MB的中点；②AN＝BM；③P为AB的中点；④AB＝6PM.其中正确的有(　 　)

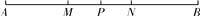
    A. 1个 B. 2个 C. 3个 D. 4个

    D 【解析】∵M、N为线段AB的三等分点，∴AB=3AM=3MN=3BN， ∴M为AN的中点，N为MB的中点，故①正确， ∵AN=AM+MN，BM=BN+MN，∴AN=BM，故②正确， ∵P为MN的中点，∴MN=2MP=2NP，∴AM+MP=BN+PN，即AP=BP，∴P为AB中点，故③正确， ∵AB=3MN，MN=2PM，∴AB=6PM，故④正确， 所以正确的...

    查看答案和解析>>

    科目：初中数学 来源：浙江省宁波市2017-2018学年七年级上册期末模拟数学试卷 题型：填空题

    ①一段烟囱（无烟囱帽）；②一段圆钢；③铅锤；④烟囱帽．①②都呈________的形状；③④都呈________的形状．

    圆柱 圆锥 【解析】联系生活实际，结合几何体的概念，可知①②都承圆柱的形状，③④都呈圆锥的形状. 故答案为：圆柱，圆锥.

    查看答案和解析>>

    同步练习册答案