练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    二次函数y＝x2的图象是一条______，它的开口向上，对称轴为______，顶点坐标为______．

    抛物线 y轴 (0，0)． 【解析】试题分析：二次函数y＝x2的图像是抛物线，a>0，开口向上，b=0,关于y轴对称，c=0，顶点坐标为原点（0,0）.故答案为(1). 抛物线 (2). y轴 (3). (0，0)．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：人教七年级下册数学第九章-不等式与不等式组单元测试 题型：单选题

    从甲地到乙地有16千米，某人以4千米/时～8千米/时的速度由甲地到乙地，则他用的时间大约为（　　）

    A．1小时～2小时 B．2小时～3小时

    C．3小时～4小时 D．2小时～4小时

    D 【解析】路程一定，速度的范围直接决定所用时间的范围.

    查看答案和解析>>

    科目：初中数学 来源：2017年秋（北师大版）九年级数学下册（河南）检测：2.2　二次函数的图象与性质 题型：单选题

    任给一些不同的实数n，得到不同的抛物线y=2x2+n，如当n=0，±2时，关于这些抛物线有以下结论：①开口方向都相同；②对称轴都相同；③形状都相同；④都有最低点，其中判断正确的个数是（ ）

    A．1个 B．2个 C．3个 D．4个

    D． 【解析】 试题分析：∵当a＞0时，开口向上，当a＜0时，开口向下； ①此题a=2＞0，所以开口向上，正确； ②对称轴为y轴，所以正确； ③因为a相同，所以开口方向、形状都相同，正确； ④因为a=2＞0，所以开口向上，有最低点．正确； 所以判断正确的个数是4个． 故选D．

    查看答案和解析>>

    科目：初中数学 来源：2017年秋（北师大版）九年级数学下册（河南）检测：2.2　二次函数的图象与性质 题型：填空题

    当－1≤x≤3时，二次函数y＝－x2的最小值是_____，最大值是______．

    －9 0 【解析】试题分析：二次函数y＝－x2对称轴为y轴，开口向下，在y轴左边y随x的增大而增大，在y轴右边，y随x的增大而减小。所以当－1≤x≤3时，最小值是当x=3时，y=-9;最大值是当x=0时，y=0.故答案为：-9,0.

    查看答案和解析>>

    科目：初中数学 来源：2017年秋（北师大版）九年级数学下册（河南）检测：2.2　二次函数的图象与性质 题型：单选题

    抛物线y＝2x2，y＝－2x2，y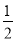＝x2的共同性质是( )

    A. 开口向上 B. 对称轴是y轴

    C. 都有最高点 D. y随x的增大而增大

    B 【解析】试题分析：观察抛物线y＝2x2，y＝－2x2，y＝x2，发现三个抛物线b=0,c=0，所以他们的对称轴均为y轴；三个函数a的正负不同所以开口方向不同；开口向上的有最低点，开口向下的有最高点；三个函数在不同的定义域内，增减性不同，并不是单调递增的.故选B.

    查看答案和解析>>

    科目：初中数学 来源：上海市浦东新区第四教育署2017-2018学年八年级（五四学制）上学期期中质量调研数学试卷 题型：解答题

    某校的分校区规划时决定在长为32米，宽为20米的长方形草坪中央修筑同样宽的两条互相垂直的小路，把长方形草坪分割成同样面积的的四块小草坪，每块小草坪的面积为135平方米，问道路的宽是多少米？

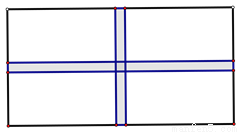
    道路的宽度为2米. 【解析】试题分析：把四块耕地拼到一起正好构成一个矩形，矩形的长和宽分别是（32-x）和（20-x），根据矩形的面积公式，列出关于道路宽的方程求解． 试题解析：设道路的宽度为x米. 由题意得， （32-x）（20-x）=135×4 整理得， x2-52x+100=0 x1=2，x2=50不合题意，舍去 ∴. 答：道路的宽度为2米. ...

    查看答案和解析>>

    科目：初中数学 来源：上海市浦东新区第四教育署2017-2018学年八年级（五四学制）上学期期中质量调研数学试卷 题型：填空题

    一家今年刚成立的小型快递公司业务量逐月攀升，今年7月份和9月份完成投送的快递件数分别是20万件和24.2万件.若假设该公司每月投送的快递件数的增长率相同，则这家公司投送快递件数的月平均增长率为 ________________．

    10% 【解析】试题解析：设该快递公司投递总件数的月平均增长率为x，根据“今年7月份与9月份完成投递的快递总件数分别为20万件和24.2万件，现假定该公司每月投递的快递总件数的增长率相同”建立方程为： 20（1+x）2=24.2， 解得x1=0.1，x2=-2.1（不合题意舍去）． 即该快递公司投递总件数的月平均增长率为10%.

    查看答案和解析>>

    科目：初中数学 来源：湖南省耒阳市冠湘学校2018届九年级上学期第二次段考（期中）考试数学试卷 题型：解答题

    如图，利用一面墙(墙的长度不超过45m)，用80m长的篱笆围一个矩形场地．

    (1)怎样围才能使矩形场地的面积为750m2？

    (2)能否使所围矩形场地的面积为810m2 ，为什么？

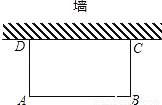
    （1）当所围矩形的长为30m、宽为25m时，能使矩形的面积为750m2（2）不能 【解析】试题分析：（1）设所围矩形ABCD的长AB为x米，则宽AD为（80-x）米，根据矩形面积的计算方法列出方程求解； （2）假使矩形面积为810，则x无实数根，所以不能围成矩形场地． 试题解析：【解析】 （1）设所围矩形ABCD的长AB为x米，则宽AD为（80-x）米． 依题意，得x•（...

    查看答案和解析>>

    科目：初中数学 来源：黑龙江省大庆市（五四制）2017-2018学年七年级上学期期中考试数学试卷 题型：填空题

    已知一个角的补角是130º，则这个角的度数是________

    50° 【解析】180°?130°=50°， 那么这个角的余角的度数是90°?50°=40°. 故答案为：40°.

    查看答案和解析>>

    同步练习册答案