
从甲地到乙地有16千米,某人以4千米/时~8千米/时的速度由甲地到乙地,则他用的时间大约为( )
A.1小时~2小时 B.2小时~3小时
C.3小时~4小时 D.2小时~4小时
D 【解析】路程一定,速度的范围直接决定所用时间的范围.科目:初中数学 来源:2017年秋(北师大版)九年级数学下册(河南)检测:3.9 弧长及扇形的面积 题型:单选题
钟面上的分针的长为1,从9点到9点30分,分针在钟面上扫过的面积是( )
A. 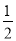 π B.
π B. 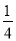 π C.
π C. 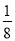 π D. π
π D. π
查看答案和解析>>
科目:初中数学 来源:湖南省醴陵市青云学校2016-2017学年七年级上学期期中考试数学试卷 题型:单选题
如图所示,下列判断正确的是( )

A. 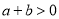 B.
B. 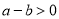
C. 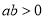 D.
D. 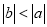
查看答案和解析>>
科目:初中数学 来源:人教七年级下册数学第九章-不等式与不等式组单元测试 题型:填空题
已知x=3是方程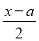 —2=x—1的解,那么不等式(2—
—2=x—1的解,那么不等式(2—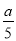 )x<
)x<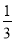 的解集是______.
的解集是______.
查看答案和解析>>
科目:初中数学 来源:人教七年级下册数学第九章-不等式与不等式组单元测试 题型:单选题
某种出租车的收费标准:起步价7元(即行驶距离不超过3千米都需付7元车费),超过3千米后,每增加1千米,加收2.4元(不足1千米按1千米计).某人乘这种出租车从甲地到乙地共付车费19元,那么甲地到乙地路程的最大值是( ).
A. 5千米 B. 7千米 C. 8千米 D. 15千米
C 【解析】试题分析:本题可先用19减去7得到12,则2.4(x﹣3)≤12,解出x的值,取最大整数即为本题的解. 【解析】 依题意得:2.4(x﹣3)≤19﹣7, 则2.4x﹣7.2≤12, 即2.4x≤19.2, ∴x≤8. 因此x的最大值为8. 故选:C.查看答案和解析>>
科目:初中数学 来源:2017年秋(北师大版)九年级数学下册(河南)检测:2.2 二次函数的图象与性质 题型:解答题
如果二次函数的二次项系数为1,那么此二次函数可表示为y=x2+px+q,我们称[p,q]为此函数的特征数,如函数y=x2+2x+3的特征数是[2,3].
(1)若一个函数的特征数为[-2,1],求此函数图象的顶点坐标;
(2)探究下列问题:
①若一个函数的特征数为[4,-1],将此函数的图象先向右平移1个单位长度,再向上平移1个单位长度,求得到的图象对应的函数的特征数;
②若一个函数的特征数为[2,3],问此函数的图象经过怎样的平移,才能使得到的图象对应的函数的特征数为[3,4]?
(1) (1,0);(2) ① [2,-3],②见解析 【解析】试题分析:首先根据函数的特征数可以确定函数表达式为y=x2-2x+1=(x-1)2,所以可得出顶点坐标为:(1,0);先根据函数的特征数写出函数的表达式,将表达式写成顶点式,然后再平移,平移时规律为左加右减,上加下减。求出平移后的函数表达式是顶点式,将顶点式化成y=x2+px+q的形式,即可求得特征数;如果已知两个函数的特征数,...查看答案和解析>>
科目:初中数学 来源:2017年秋(北师大版)九年级数学下册(河南)检测:2.2 二次函数的图象与性质 题型:解答题
已知,在同一平面直角坐标系中,正比例函数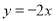 与二次函数y=-x2+2x+c的图象交于点A(-1,m).
与二次函数y=-x2+2x+c的图象交于点A(-1,m).
(1)求m,c的值;
(2)求二次函数图象的对称轴和顶点坐标.
(1) 5; (2) (1,6). 【解析】(1)将点A的坐标(-1,m)代入正比例函数的解析式求出m的值,再将求出的点A的坐标代入二次函数的解析式就可以求出c的值; (2)将求出的二次函数的解析式的一般式化为顶点式就直接求出抛物线的对称轴和顶点坐标. 【解析】 (1)∵点A在正比例函数的图象上, ∴m==2 ∴点A坐标为(-1,2). ∵点A在二次函数图象上...查看答案和解析>>
科目:初中数学 来源:2017年秋(北师大版)九年级数学下册(河南)检测:2.2 二次函数的图象与性质 题型:填空题
把抛物线y=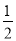 (x-1)2+2向左平移1个单位长度,再向下平移2个单位长度,则所得抛物线的表达式为________.
(x-1)2+2向左平移1个单位长度,再向下平移2个单位长度,则所得抛物线的表达式为________.
查看答案和解析>>
科目:初中数学 来源:2017年秋(北师大版)九年级数学下册(河南)检测:2.2 二次函数的图象与性质 题型:填空题
二次函数y=x2的图象是一条______,它的开口向上,对称轴为______,顶点坐标为______.
抛物线 y轴 (0,0). 【解析】试题分析:二次函数y=x2的图像是抛物线,a>0,开口向上,b=0,关于y轴对称,c=0,顶点坐标为原点(0,0).故答案为(1). 抛物线 (2). y轴 (3). (0,0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com