
已知线段a=1,c=5,线段b是线段a,c的比例中项,则线段b的值为________
【解析】试题解析:∵线段b是线段a、c的比例中项, ∴b2=ac, 即b2=1×5,解得b=-(舍去)或b=, ∴线段b的值为. 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:2017-2018学年七年级数学下册(遵义):期中检测题 题型:单选题
文文设计了一个关于实数运算的程序,按此程序,输入一个数后,输出的数比输入的数的平方小1,若输入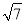 ,则输出的结果为【 】
,则输出的结果为【 】
A. 5 B. 6 C. 7 D. 8
B 【解析】根据运算程序得出输出数的式子,再根据实数的运算计算出此数即可: ∵输入一个数后,输出的数比输入的数的平方小1, ∴输入,则输出的结果为()2﹣1=7﹣1=6。故选B。查看答案和解析>>
科目:初中数学 来源:山东省潍坊市高密市2017-2018学年七年级(上)期中数学试卷 题型:填空题
a,b中数轴上的位置如图所示,则a,b,﹣a,﹣b的大小顺序是_____.

查看答案和解析>>
科目:初中数学 来源:山东省潍坊市高密市2017-2018学年七年级(上)期中数学试卷 题型:单选题
既是分数又是正有理数的是( )
A. +2 B. ﹣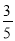 C. 0 D. 2.015
C. 0 D. 2.015
查看答案和解析>>
科目:初中数学 来源:浙江省余姚市2018届九年级上学期期中考试数学试卷 题型:解答题
已知抛物线y=ax2+bx+c经过(-1,0),(0,-3),(2,-3)三点.
(1)求这条抛物线的解析式;
(2)写出抛物线的开口方向、对称轴和顶点坐标.
(1)y=x2-2x-3 (2)开口向上,对称轴是直线x=1,顶点坐标(1,-4) 【解析】试题分析:已知抛物线上三点坐标,可用待定系数法求出抛物线的解析式;进而可根据函数的解析式求出抛物线的开口方向,及对称轴方程与顶点坐标(用配方法或公式法求解均可). 试题解析:(1)把(-1,0),(0,-3),(2,-3)代入y=ax2+bx+c, 得: 解得: , 则抛物线的...查看答案和解析>>
科目:初中数学 来源:云南省2017-2018学年七年级上学期期中考试数学试卷 题型:解答题
某地电话拨号上网有两种收费方式,用户可以任选其一:计时制,每分钟0.05元;包月制,每月50元(只限一部宅电上网).此外,每种上网方式都要加收通信费每分钟0.02元.
(1)某用户某月上网的时间为a小时,请你写出两种收费方式下该用户应支付的费用;
(2)若某用户估计一个月内上网的时间为20小时,你认为选择哪种上网方式较合算?
(1)方式一费用:4.2a,方式二费用:5+1.2a;(2)方式二上网较合算. 【解析】试题分析:(1)依次写出两种计费方式的费用,注意单位;(2)将a=20分别代入两种方式,比较得出的结果,花费少的合算. 试题解析: (1)方式一:0.05a×60+0.02a×60=4.2a; 方式二:50+0.02a×60=50+1.2a, (2)方式一:4.2×20=84; ...查看答案和解析>>
科目:初中数学 来源:云南省2017-2018学年七年级上学期期中考试数学试卷 题型:解答题
计算:
(1)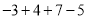 (2)
(2)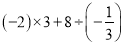
(3)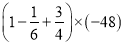 (4)
(4)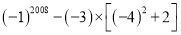
查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年第一学期初二数学期中试卷 题型:解答题
已知AB//DE,BE=CF,AB=DE,∠A=∠D.
求证:AC//DF.
证明:
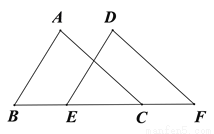
查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年第一学期八年级数学期中试卷 题型:解答题
计算:
(1) 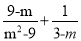 (2)
(2) 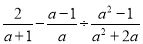
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com