练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知抛物线y=ax2＋bx＋c经过（－1，0），（0，－3），（2，－3）三点．

    （1）求这条抛物线的解析式；

    （2）写出抛物线的开口方向、对称轴和顶点坐标．

    （1）y=x2-2x-3 （2）开口向上，对称轴是直线x=1，顶点坐标（1，-4） 【解析】试题分析：已知抛物线上三点坐标，可用待定系数法求出抛物线的解析式；进而可根据函数的解析式求出抛物线的开口方向，及对称轴方程与顶点坐标（用配方法或公式法求解均可）． 试题解析：（1）把（-1，0），（0，-3），（2，-3）代入y=ax2+bx+c， 得： 解得： ， 则抛物线的...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017-2018学年七年级数学下册（遵义）：期中检测题 题型：填空题

    (1)计算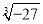： ＝________；(2)点(2，－3)到x轴的距离为________．

    （1）-3 （2）3 【解析】试题解析：（1）＝-3； （2）点（2，-3）到x轴的距离为|-3|=3． 故答案为：-3；3.

    查看答案和解析>>

    科目：初中数学 来源：山东省潍坊市高密市2017-2018学年七年级（上）期中数学试卷 题型：解答题

    如图所示，B，C两点把线段AD分成4：5：7的三部分，E是线段AD的中点，CD=14厘米．

    （1）求EC的长．

    （2）求AB：BE的值．

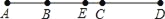
    EC长是2厘米，AB：BE的值是1 【解析】试题分析：（1）由题意知，B，C两点把线段AD分成4：5：7三部分，则令AB，BC，CD分别为4x厘米，5x厘米，7x厘米．根据CD=14厘米，得出x=2．根据E是线段AD的中点，可得ED=AD=16厘米，代入EC=ED﹣CD可求； （2）分别求出AB，BE的长后计算AB：BE的值． 试题解析：设线段AB，BC，CD分别为4x厘米，5x...

    查看答案和解析>>

    科目：初中数学 来源：山东省潍坊市高密市2017-2018学年七年级（上）期中数学试卷 题型：单选题

    为了了解某市参加中考的13000名学生体重情况，抽查了其中1600名学生的体重进行统计分析，下列叙述正确的是（　　）

    A. 13000名学生是总体

    B. 1600名学生的体重是总体的一个样本

    C. 每名学生的体重是总体的一个样本

    D. 以上调查是普查

    B 【解析】总体是指考查的对象的全体，个体是总体中的每一个考查的对象，样本是总体中所抽取的一部分个体，而样本容量则是指样本中个体的数目．我们在区分总体、个体、样本、样本容量，这四个概念时，首先找出考查的对象．从而找出总体、个体．再根据被收集数据的这一部分对象找出样本，最后再根据样本确定出样本容量．可得： A、13000名学生体重是总体，故A不符合题意； B、1600名学生的体重是...

    查看答案和解析>>

    科目：初中数学 来源：浙江省余姚市2018届九年级上学期期中考试数学试卷 题型：解答题

    某超市经销一种销售成本为每件60元的商品，据市场调查发现，如果按每件70元销售，一周能售出500件，若销售单价每涨1元，每周销售就减少10件，设销售价为每件x元（x≥70），一周的销售量为y件.

    （1）当销售价为每件80元时，一周能销售多少件？答：_____________件．

    （2）写出y与x的函数关系式，并写出x的取值范围.

    （3）设一周的销售利润为w，写出w与x的函数关系式.

    （4）在超市对该种商品投入不超过18000元的情况下，使得一周销售利润达到8000元，销售单价应定为多少？

    （1）400； （2），(70≤x≤120)； （3）； （4）销售单价应定为100元 【解析】试题分析：（1）根据题意单价为80元时，销售量减少了10（80-70）=100件，所以每周销售400件；（2）根据题意可得y=500-10（x-70），由实际意义得出x的范围；（3）利润=(售价-进价) ×销售量可得关系式；（4）令y=8000，求出x的实际取值． 试题解析...

    查看答案和解析>>

    科目：初中数学 来源：浙江省余姚市2018届九年级上学期期中考试数学试卷 题型：填空题

    已知线段a＝1，c＝5，线段b是线段a，c的比例中项，则线段b的值为________

    【解析】试题解析：∵线段b是线段a、c的比例中项， ∴b2=ac， 即b2=1×5，解得b=-（舍去）或b=， ∴线段b的值为．

    查看答案和解析>>

    科目：初中数学 来源：云南省2017-2018学年七年级上学期期中考试数学试卷 题型：解答题

    学习了有理数的乘法后，老师给同学们布置这样一道题目：计算49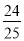 ×（–5），看谁算的又快又对，有三位同学的解法如下：

    小军：原式 =（49 + 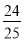）×（–5）= 49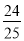×（–5）+ ×（–5）

    =–245–4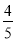=–249；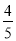

    小明：原式 = –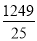 × 5 = – 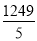= – 249 ；

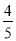    小丽：原式 =（49 + 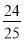）×（-5）=（50 -1 + 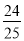）×（-5）

    =（50 - 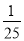）×（-5）= 50 ×（-5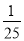）+（ - ） ×（-5）

    = –250 +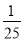= –249；

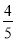    （1）对于以上三种解法，你认为谁的解法较好？

    （2）上面的解法对你有何启发，用你认为最合适的方法计算：

    　19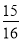 ×（– 8）

    （1）小丽的解法好一点；（2）． 【解析】试题分析：（1）比较三个人的方法，小军和小明的方法没有小丽的简单；（2）先将19写成20－，再用乘法分配律展开计算出结果即可. 试题解析： （1）小丽的方法较好； （2）19 ×（－8）=（20－）×（－8）=20×（－8）－×（－8）=－160+=－159.

    查看答案和解析>>

    科目：初中数学 来源：云南省2017-2018学年七年级上学期期中考试数学试卷 题型：单选题

    下列合并同类项的计算中，错误的个数有（　　）

    ① 3y- 2y=1； ②x2+x2=x4； ③ 3mn-3mn=0；④4ab2-5ab2=-ab2； ⑤ 3m2+4m3=7m5．

    A. 4个 B. 3个 C. 2个 D. 1个

    B 【解析】3y－2y=y，所以①错误；x2+x2=2x2，所以②错误；3mn-3mn=0，所以③正确；4ab2－5ab2=－ab2，所以④正确；3m2+4m3≠7m5，所以⑤错误. 故选B.

    查看答案和解析>>

    科目：初中数学 来源：北京市2017-2018学年第一学期八年级数学期中试卷 题型：解答题

    如图，点E、F在BC上，BE=CF，AB=DC，AF=DE．

    求证：∠B=∠C

    证明：∵BE=CF

    ∴BE +______ = CF +______

    即______=_______

    在△ABF和△DCE中

    ∴△ABF≌△DCE（ ）

    ∴∠B=∠C（ ）

    见解析 【解析】试题分析：只要证明△ABF≌△DCE，写出理由即可解决问题． 试题解析：【解析】 ∵BE=CF，∴BE+EF=CF+EF，即BF=EC，在△ABE和△DCE中， ，∴△ABF≌△DCE（SSS），∴∠B=∠C（全等三角形的对应角相等）． 故答案为：EF，EF，BF，CE，SSS，全等三角形的对应角相等．

    查看答案和解析>>

    同步练习册答案